题目内容

10．已知三个命题如下：
①所有的素数都是奇数； 
②?x∈R，（x-1）2+1≥1；
③有的无理数的平方还是无理数．
则这三个命题中既是全称命题又是真命题的个数是（　　）
A．0B．1C．2D．3

分析 先找出全称命题，然后再根据各自的性质判断真假．①素数又叫做质数，质数与合数是根据一个数因数的故数的多少来进行分类，奇数与偶数是根据是不是2的倍数来进行分类的；最小的素数（质数）是2，2是偶数；由此解答．②③均由概念或者公理判定．

解答 解：对于①最小的素数（质数）是2，2是偶数不是奇数，因此所有的素数都是奇数，这种说法是错误的．故①不满足条件
对于②因?x∈R，（x-1）2≥0，所以（x-1）2+1≥1，所以②为真命题．由全称命题和特称命题的定义知②是全称命题．故②满足条件．
对于③有的无理数的平方还是无理数该命题时真命题，但是存在性命题．故③不满足条件
故选：B

点评 本题主要考查全称命题和特称命题的概念及素数、无理数的概念是解答该题的关键，属于基础题型．

练习册系列答案
相关题目
20．某学习兴趣小组开展“学生语文成绩与英语成绩的关系”的课题研究，对该校高二年级800名学生上学期期末语文和英语成绩进行统计，按优秀和不优秀进行分类．记集合A={语文成绩优秀的学生}，B={英语成绩优秀的学生}．如果用card（M）表示有限集合M中元素的个数．已知card（A∩B）=60，card（A∩CUB）=140，card（CUA∩B）=100，其中U表示800名学生组成的全集．
（Ⅰ）是否有99.9%的把握认为“该校学生的语文成绩与英语成绩优秀与否有关系”；
（Ⅱ）将上述调查所得的频率视为概率，从该校高二年级的学生成绩中，有放回地随机抽取3次，记所抽取的成绩中，语文英语两科成绩中至少有一科优秀的人数为x，求x的分布列和数学期望．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
参考数据：
P（K2≥k0）0.0250.0100.0050.001
k05.0246.6357.87910.828
1．一个立方体骰子的六个面分别标有数字1，2，2，3，3，4；另一个立方体骰子的六个面分别标有数字1，3，4，5，6，8．掷两粒骰子，则其最上面所标的两数之和为7的概率是$\frac{1}{6}$．
18．已知函数f（x）=ln|x|-x2+ax，其中a∈R．
（1）当a=1时，求函数的单调增区间．
（2）l为f（x）在x=x0处的切线，且f（x）图象上的点都不在l的上方，求x0的取值范围．
5．已知数列{an}是等差数列且公差d＞0，n∈N*，a1=2，a3为a1和a9的等比中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设${b_n}=\frac{2}{{n（{{a_n}+2}）}}$，求数列{bn}的前n项和Sn．
15．一种智能手机电子阅读器，特别设置了一个“健康阅读”按钮，在开始阅读或者阅读期间的任意时刻按下“健康阅读”按钮后，手机阅读界面的背景会变为蓝色或绿色以保护阅读者的视力．假设“健康阅读”按钮第一次按下后，出现蓝色背景与绿色背景的概率都是$\frac{1}{2}$．从按钮第二次按下起，若前次出现蓝色背景，则下一次出现蓝色背景、绿色背景的概率分别为$\frac{1}{3}$、$\frac{2}{3}$；若前次出现绿色背景，则下一次出现蓝色背景、绿色背景的概率分别为$\frac{3}{5}$、$\frac{2}{5}$．记第n（n∈N，n≥1）次按下“健康阅读”按钮后出现蓝色背景概率为Pn．
（Ⅰ）求P2的值；
（Ⅱ）当n∈N，n≥2时，试用Pn-1表示Pn；
（Ⅲ）求Pn关于n的表达式．
2．已知各项均为正数的等比数列{an}中，3a1，$\frac{1}{2}$a3，2a2，成等差数列，则$\frac{{a}_{2014}+{a}_{2015}}{{a}_{2011}+{a}_{2012}}$=（　　）
A．-1或3B．3C．27D．-1或27
19．已知直线m，n和平面α，则m∥n的必要不充分条件是（　　）
A．直线m，n和平面α成等角B．m⊥α且n⊥α
C．m∥α且n?αD．m∥α且n∥α
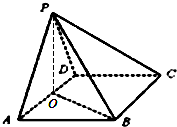20．如图，在四棱锥P-ABCD中，底面ABCD为菱形且∠DAB=60°，O为AD中点．
（Ⅰ）若PA=PD，求证：平面POB⊥平面PAD；
（Ⅱ）试问在线段BC上是否存在点M，使DM∥面POB，如存在，指出M的位置，如不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网