题目内容

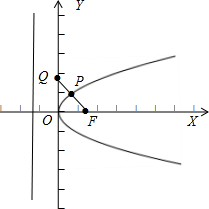
F是抛物线y2=2px（p＞0）的焦点，P是抛物线上一点，FP延长线交y轴于Q，若P恰好是FQ的中点，则|PF|=（　　）
A．
p
3
B．
2
3
p		C．pD．
3
4
p
由于F是抛物线y2=2px（p＞0）的焦点，
则点F为（
p
2
，0），
又由P是抛物线上一点，FP延长线交y轴于Q，P恰好是FQ的中点，
则点P的横坐标为
p
4
，故P到准线的距离为
p
4
-(-
p
2
)=
3p
4
，
根据抛物线的定义可知|PF|即为P到准线的距离，
∴|PF|=
3p
4
．
故选：D．
练习册系列答案
相关题目
已知直线l1：4x-3y+8=0和直线l2：x=-1，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是（　　）
A．
12
5
B．3C．2D．
37
16
曲线C是平面内与定点F（2，0）和定直线x=-2的距离的积等于4的点的轨迹．给出下列四个结论：
①曲线C过坐标原点；
②曲线C关于x轴对称；
③曲线C与y轴有3个交点；
④若点M在曲线C上，则|MF|的最小值为2(
2
-1)．
其中，所有正确结论的序号是______．
已知点P（0，2），抛物线C：y2=2px（p＞0）的焦点为F，线段PF与抛物线C的交点为M，过M作抛物线准线的垂线，垂足为Q．若∠PQF=90°，则p=______．
下列说法中，正确的有______．
①若点P（x0，y0）是抛物线y2=2px上一点，则该点到抛物线的焦点F的距离是|PF|=x0+
P
2
；
②方程x2+y2-2x+1=0表示的图形是圆；
③设定圆O上有一动点A，圆O内一定点M，AM的垂直平分线与半径OA的交点为点P，则P的轨迹为一椭圆；
④某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=13；
⑤双曲线
y2
49
-
x2
25
=-1的渐近线方程是y=±
5
7
x．
抛物线y=2x2的准线方程为（　　）
A．y=
1
4
B．y=
1
8
C．y=-
1
4
D．y=-
1
8
若抛物线y2=4x的准线也是双曲线
x2
a2
-
4y2
3
=1的一条准线，则该双曲线的渐近线方程为（　　）
A．y=±2xB．y=±
2
2
x		C．y=±
3
x		D．y=±
2
x
已知等边三角形的一个顶点在坐标原点，另外两个顶点在抛物线y2=2x上，则该三角形的面积是______．
若抛物线y2=x上两点A（x1，y1）、B（x2，y2）关于直线y=x+b对称，且y1y2=-1，则实数b的值为（　　）
A．-3B．3C．2D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网