题目内容
(本小题满分14分)
已知抛物线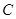 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在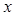 轴上. 且经过点
轴上. 且经过点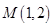 ,
,
(1)求抛物线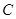 的方程;
的方程;
(2)若动直线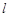 过点
过点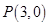 ,交抛物线
,交抛物线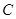 于
于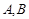 两点,是否存在垂直于
两点,是否存在垂直于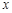 轴的直线
轴的直线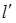 被以
被以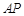 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出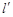 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知抛物线
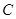 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在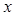 轴上. 且经过点
轴上. 且经过点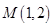 ,
,(1)求抛物线
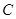 的方程;
的方程;(2)若动直线
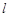 过点
过点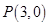 ,交抛物线
,交抛物线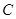 于
于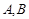 两点,是否存在垂直于
两点,是否存在垂直于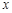 轴的直线
轴的直线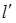 被以
被以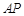 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出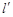 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. (1)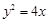 (2)存在,
(2)存在,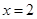
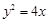 (2)存在,
(2)存在,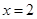
试题分析:(1)设抛物线方程为
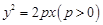 ,
,将
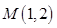 代入方程得
代入方程得 ,
, . ……4分
. ……4分(2)设
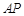 的中点为
的中点为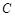 ,
,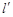 的方程为:
的方程为: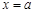 ,以
,以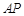 为直径的圆交
为直径的圆交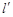 于
于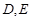 两点,
两点,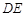 中点为
中点为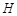 ,设
,设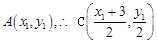 , ……8分
, ……8分 ,
,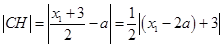

 ……12分
……12分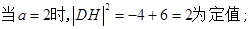
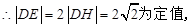
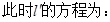 .
.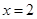 . ……14分
. ……14分点评:圆锥曲线的题目是每年高考必考的题目,一般运算量较大,需要较强的运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与直线
与直线 围成的封闭图形的面积是( )
围成的封闭图形的面积是( )



 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
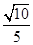


 与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为 

 上一点
上一点 到它的右焦点距离为
到它的右焦点距离为 ,那么
,那么 
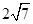


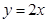 ,焦距为
,焦距为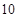 ,这双曲线的方程为___
,这双曲线的方程为___  时的椭圆的标准方程是 .
时的椭圆的标准方程是 . 为椭圆
为椭圆 的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为 为线段
为线段 的中点,则
的中点,则 ( )
( ) ,
, 为抛物线上一点,
为抛物线上一点, 为
为 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.(1)若
为坐标原点.(1)若 ,求
,求 交抛物线
交抛物线 于
于 两点, 且斜率分别为
两点, 且斜率分别为 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.