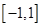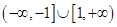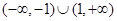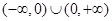题目内容
设函数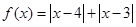 ,
,
(1)求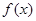 的最小值
的最小值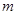 ;
;
(2)当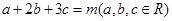 时,求
时,求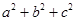 的最小值.
的最小值.
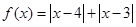 ,
,(1)求
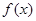 的最小值
的最小值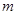 ;
;(2)当
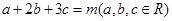 时,求
时,求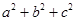 的最小值.
的最小值.(1)1;(2)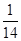
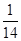
试题分析:(1)因为
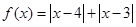 ,所以通过绝对值的基本不等式
,所以通过绝对值的基本不等式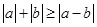 ,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.
,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.(2)由(1)求出的
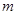 的值,所以得到
的值,所以得到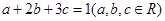 .再根据柯西不等式即可求得
.再根据柯西不等式即可求得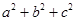 的最小值.同时强调等号成立的条件.
的最小值.同时强调等号成立的条件.试题解析:(1)法1: f(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,
故函数f(x)的最小值为1. m="1." 法2:
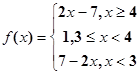 . x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,故函数f(x)的最小值为1. m="1."
. x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,故函数f(x)的最小值为1. m="1." (2)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1故a2+b2+c2≥
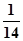
当且仅当
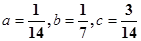 时取等号
时取等号
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
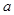 2+
2+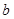 2恒成立,试求2
2恒成立,试求2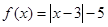 ,
,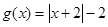 。
。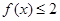 的解集;
的解集;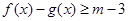 有解,求实数
有解,求实数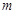 的取值范围。
的取值范围。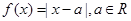
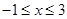 时,
时,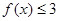 ,求a的取值范围;
,求a的取值范围;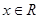 ,
,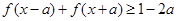 恒成立,求实数a的最小值
恒成立,求实数a的最小值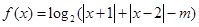 .若关于
.若关于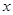 的不等式
的不等式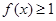 的解集是
的解集是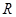 ,则
,则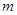 的取值范围是 .
的取值范围是 .  在
在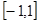 区间上恒有意义,则
区间上恒有意义,则 的取值范围是( )
的取值范围是( )