题目内容
18.图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第n个图形包含f(n)个“福娃迎迎”.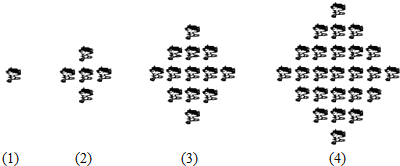
(1)求出f(5);
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式(不需写出证明过程);
(3)根据你得到的关系式求f(n)的表达式.
分析 (1)由题意,可以求出f(5);
(2)考查相邻两项的关系可得出f(n+1)-f(n)=4n;
(3)由累加法可求得f(n)=2n2-2n+1,由此可求出答案.
解答 解:(1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,
∴f(5)=25+4×4=41.…(4分)
(2)∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n.…(10分)
(3)∵f(2)-f(1)=4×1,f(3)-f(2)=4×2,f(4)-f(3)=4×3,f(n-1)-f(n-2)=4•(n-2),f(n)-f(n-1)=4•(n-1),
∴f(n)-f(1)=4[1+2++(n-2)+(n-1)]=2(n-1)•n,…(14分)
∴f(n)=2n2-2n+1(n≥2),
∵f(1)=1也满足上式,∴f(n)=2n2-2n+1. …(16分)
点评 本题考查归纳推理,解题的关键是研究相邻两项的关系得出递推公式,再由累加法得出项的表达式,本题考查了分析归纳的能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
7.为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=7.01,则认为“喜欢乡村音乐与性别有关系”有( )以上的把握.
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.1% | B. | 1% | C. | 99% | D. | 99.9% |
6.若要做一个正六棱锥形的铁皮烟囱帽,底口边长为0.4m,高为0.5m,则下列各数中与所需要的铁皮面积数最接近的是( )
| A. | 0.73 m2 | B. | 1.62 m2 | C. | 1.78 m2 | D. | 2.63 m2. |
13.“a>b”是“ac2>bc2”成立的( )
| A. | 充分而非必要条件 | B. | 必要而非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
10.若(1-m)+(3m+2)i是纯虚数,则实数m的值为( )
| A. | 1 | B. | 1或2 | C. | 0 | D. | -1、1、2 |
7.已知z∈C,|z-2|=1,则|z+2+5i|的最大值和最小值分别是( )
| A. | $\sqrt{41}$+1和$\sqrt{41}$-1 | B. | 3和1 | C. | 5$\sqrt{2}$和$\sqrt{34}$ | D. | $\sqrt{39}$和3 |