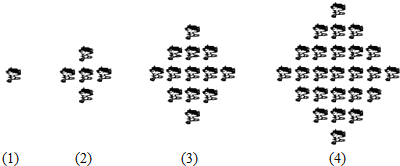题目内容
7.已知z∈C,|z-2|=1,则|z+2+5i|的最大值和最小值分别是( )| A. | $\sqrt{41}$+1和$\sqrt{41}$-1 | B. | 3和1 | C. | 5$\sqrt{2}$和$\sqrt{34}$ | D. | $\sqrt{39}$和3 |
分析 根据复数运算的几何意义,求出最值.
解答 解:z∈C,|z-2|=1,设z=x+yi,则表示z在以(2,0)为圆心1为半径的圆上,
则|z+2+5i|表示z到(-2,-5)的距离,所以它的最大值为$\sqrt{(2+2)^{2}+(-5)^{2}}+1=\sqrt{41}+1$,和最小值$\sqrt{(2+2)^{2}+(-5)^{2}}-1=\sqrt{41}-1$;
故选:A.
点评 本题考查了复数运算的几何意义的运用;关键是明确已知等式和所求的几何意义.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.如图所示,一个类似杨辉三角的数阵,则第n(n≥2)行的第2个数为( )


| A. | n2+2n+3 | B. | n2+2n-3 | C. | n2-2n+3 | D. | n2-2n-3 |
12.已知向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(x,2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的值是( )
| A. | 4 | B. | 1 | C. | -1 | D. | -4 |
19.已知条件p:|x+1|>2,条件q:5x-6>x2,则¬p是¬q的( )
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既非充分也非必要条件 |