Question

8．已知函数f（x）是定义在R上的偶函数，且当x≥0时，f（x）=x|x-2|，若关于x的方程[f（x）]²+af（x）+a+1=0（a∈R）恰好有12个不同实数解，则a的取值范围为（-1，2-2$\sqrt{2}$）．

Answer 1

分析 根据函数的奇偶性求出f（x）的解析式，令t=f（x），将方程转化为一元二次函数，由二次方程实根的分布，列出不等式组，解得即可．

解答 解：设x＜0，则-x＞0，满足表达式f（x）=x|x-2|．
∴f（-x）=-x|-x-2|=-x|x+2|，
又∵f（x）为偶函数，∴f（-x）=f（x），
∴f（x）=-x|x+2|，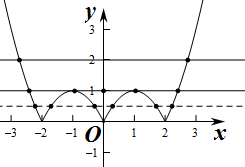
故当x＜0时，f（x）=-x|x+2|．
则f（x）=$\left\{\begin{array}{l}{x|x-2|，}&{x≥0}\\{-x|x+2|，}&{x＜0}\end{array}\right.$，
作出f（x）的图象如图：
设t=f（x），
由图象知，当t＞1时，t=f（x）有两个根，
当t=1时，t=f（x）有四个根，
当0＜t＜1时，t=f（x）有六两个根，
当t=0时，t=f（x）有三个根，
当t＜0时，t=f（x）有0个根，
则方程[f（x）]²+af（x）+a+1=0等价为t²+at+a+1=0，
若方程[f（x）]²+af（x）+a+1=0（a∈R）恰好有12个不同实数解，
等价为方程t²+at+a+1=0有两不同的根，
且0＜t₁＜1，0＜t₂＜1，
设g（t）=t²+at+a+1，
则满足$\left\{\begin{array}{l}{△={a}^{2}-4（a+1）＞0}\\{g（0）=a+1＞0}\\{g（1）=2a+2＞0}\\{0＜-\frac{a}{2}＜1}\end{array}\right.$，即$\left\{\begin{array}{l}{a＞2+2\sqrt{2}或a＜2-2\sqrt{2}}\\{a＞-1}\\{-2＜a＜0}\end{array}\right.$，
即-1＜a＜2-2$\sqrt{2}$，
则a的取值范围为（-1，2-2$\sqrt{2}$），
故答案为：（-1，2-2$\sqrt{2}$）

点评 本题考查函数的单调性和奇偶性的运用，主要考查方程与函数的零点的关系，掌握二次方程实根的分别是解题的关键．