题目内容
8．若函数f（x）=$\frac{1-2a}{x+2}$在区间（-2，+∞）递增，求实数a的取值范围．分析 利用定义法结合分式函数的性质进行求解即可．
解答 解：任取x1，x2∈（-2，+∞），且x1＜x2，…（2分）
则f（x1）-f（x2）=$\frac{1-2a}{{x}_{1}+2}$-$\frac{1-2a}{{x}_{2}+2}$=$\frac{（1-2a）（{x}_{2}-{x}_{1}）}{（{x}_{1}+2）（{x}_{2}+2）}$．…（5分）
∵函数f（x）=$\frac{1-2a}{x+2}$在区间（-2，+∞）上为增函数，
∴f（x1）-f（x2）＜0．…（7分）
∵x2-x1＞0，x1+2＞0，x2+2＞0，
∴1-2a＜0，故a＞$\frac{1}{2}$．…（10分）
即实数a的取值范围是（$\frac{1}{2}$，+∞）．…（12分）
点评 本题主要考查函数单调性的应用，利用分式函数的性质以及函数单调性的定义是解决本题的关键．
练习册系列答案
相关题目
18．（2x-$\frac{1}{x}$）4的展开式中的常数项为（ ）
| A． | 6 | B． | -6 | C． | 24 | D． | -24 |
19．某地区2009年至2013年农村居民家庭人均纯收入y（单位：千元）的数据如下表：
（1）用最小二乘法求y关于x的线性回归方程；
（2）利用（1）中的回归方程，分析2009年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.8 | 3.2 | 4.2 | 4.8 | 5 |
（2）利用（1）中的回归方程，分析2009年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
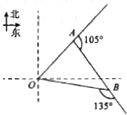如图，一只蜘蛛从点O出发沿北偏东45°方向爬行xcm，到达点A处捕捉到一只小虫，然后沿OA方向右转105°爬行10cm，到达点B处捕捉哦另一只小虫，这时他沿AB方向右转135°爬行回到它的出发点O处，那么x=$\frac{10\sqrt{6}}{3}$．
13．函数y=x3+4x的递增区间是（ ）
| A． | （0，+∞） | B． | （-∞，-2） | C． | （2，+∞） | D． | （-∞，+∞） |
3．已知a＞0，b＞0，a+b=1则-$\frac{1}{2a}-\frac{2}{b}$的最大值为（ ）
| A． | -3 | B． | -4 | C． | $-\frac{1}{4}$ | D． | $-\frac{9}{2}$ |