题目内容
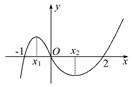
函数f(x)=x3+bx2+cx+d的大致图象如图所示,则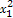 +
+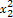 等于( )
等于( )
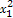 +
+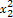 等于( )
等于( )
A. | B.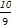 | C.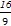 | D. |
C
【思路点拨】从函数图象上可知x1,x2为函数f(x)的极值点,故x1,x2是f'(x)=0的两根,再根据根与系数的关系进行求解.
解:从函数图象上可知x1,x2为函数f(x)的极值点,根据函数图象经过的三个特殊点求出b,c,d.根据函数图象得d=0,且f(-1)=-1+b-c=0,f(2)=8+4b+2c=0,解得b=-1,c=-2,故f'(x)=3x2-2x-2,所以x1+x2= ,x1x2=-
,x1x2=- ,所以
,所以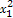 +
+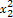 =(x1+x2)2-2x1x2=
=(x1+x2)2-2x1x2= +
+ =
=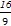 .
.
解:从函数图象上可知x1,x2为函数f(x)的极值点,根据函数图象经过的三个特殊点求出b,c,d.根据函数图象得d=0,且f(-1)=-1+b-c=0,f(2)=8+4b+2c=0,解得b=-1,c=-2,故f'(x)=3x2-2x-2,所以x1+x2=
 ,x1x2=-
,x1x2=- ,所以
,所以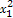 +
+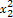 =(x1+x2)2-2x1x2=
=(x1+x2)2-2x1x2= +
+ =
=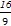 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
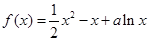 (其中
(其中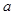 为常数).
为常数).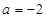 时,求函数
时,求函数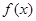 的最值;
的最值;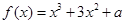 (
(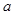 为常数),在
为常数),在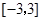 上有最小值
上有最小值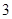 ,那么在
,那么在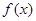 的最大值是
的最大值是  的单调递减区间是________.
的单调递减区间是________. )上是减函数,在(
)上是减函数,在(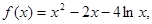 则f′(x)
则f′(x)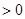 的解集为( )
的解集为( )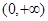
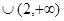
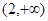
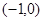
 满足
满足 ,且
,且 为偶函数,当
为偶函数,当 时,有( )
时,有( )



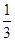 x3-
x3-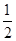 ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )
ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )