题目内容
(1)等比数列 中,对任意
中,对任意 ,
, 时都有
时都有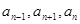 成等差,求公比
成等差,求公比 的值
的值
(2)设 是等比数列
是等比数列 的前
的前 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由
(3)设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 与
与 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由
 中,对任意
中,对任意 ,
, 时都有
时都有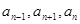 成等差,求公比
成等差,求公比 的值
的值(2)设
 是等比数列
是等比数列 的前
的前 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由(3)设等比数列
 的公比为
的公比为 ,前
,前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 与
与 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由解:(1)当 ,
, 时有
时有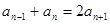

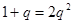
解得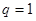 或
或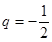 ……………………………………5分
……………………………………5分
(2)当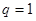 时
时
 ,显然
,显然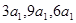 不是等差数列,
不是等差数列,
所以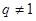 ,
,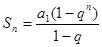
由 成等差得
成等差得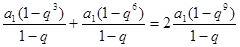
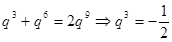 或
或 (不合题意)所以
(不合题意)所以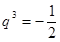 ;
;
所以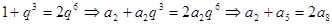
即一定有 成等差数列。…………………………………11分
成等差数列。…………………………………11分
(3)假设存在正整数 ,使
,使 成等差且
成等差且 也成等差。
也成等差。
当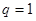 时
时
 ,显然
,显然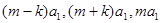 不是等差数列,
不是等差数列,
所以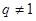 ,
,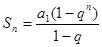 ……………………………13分
……………………………13分
由 成等差得
成等差得
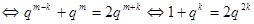
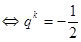 或
或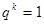 …………16分
…………16分
当 为偶数时,
为偶数时,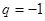 ,则有
,则有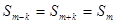 且
且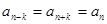 ;
;
当 为奇数时,
为奇数时,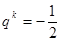 ;
;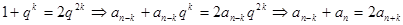 ,
,
综上所述,存在正整数 (
(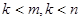 )满足题设,
)满足题设,
当 为偶数时,
为偶数时,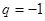 ;当
;当 为奇数时,
为奇数时,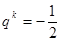 。………………………18分
。………………………18分
 ,
, 时有
时有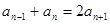

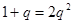
解得
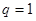 或
或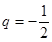 ……………………………………5分
……………………………………5分(2)当
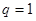 时
时
 ,显然
,显然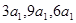 不是等差数列,
不是等差数列,所以
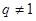 ,
,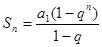
由
 成等差得
成等差得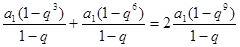
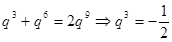 或
或 (不合题意)所以
(不合题意)所以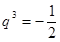 ;
;所以
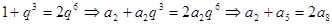
即一定有
 成等差数列。…………………………………11分
成等差数列。…………………………………11分(3)假设存在正整数
 ,使
,使 成等差且
成等差且 也成等差。
也成等差。当
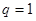 时
时
 ,显然
,显然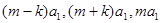 不是等差数列,
不是等差数列,所以
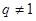 ,
,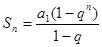 ……………………………13分
……………………………13分由
 成等差得
成等差得
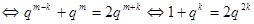
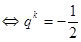 或
或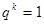 …………16分
…………16分当
 为偶数时,
为偶数时,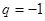 ,则有
,则有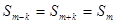 且
且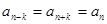 ;
;当
 为奇数时,
为奇数时,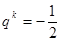 ;
;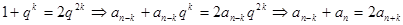 ,
,综上所述,存在正整数
 (
(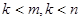 )满足题设,
)满足题设,当
 为偶数时,
为偶数时,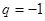 ;当
;当 为奇数时,
为奇数时,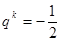 。………………………18分
。………………………18分略

练习册系列答案
相关题目
 1)小问6分,(2)小分6分.)
1)小问6分,(2)小分6分.)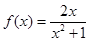 ,数列
,数列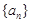 满足
满足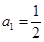 ,
,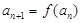 ,
,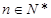 .
.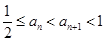 ;
;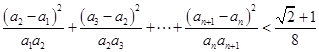 .
. 中,已知
中,已知 .
. 的通项公式;
的通项公式; 满足
满足 ,求
,求
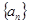 满足
满足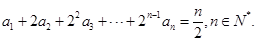
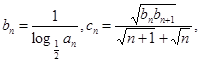 记
记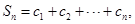 证明:Sn<1.
证明:Sn<1.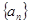 的前
的前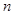 项和
项和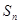 满足:
满足: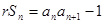 ,
,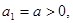 常数
常数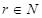
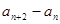 是一个定值;
是一个定值;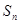 是数列
是数列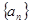 的前
的前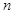 项和,
项和,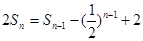 (
(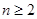 ,
,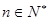 ),且
),且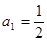 .
.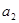 的值,并写出
的值,并写出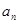 和
和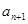 的关系式;
的关系式; 3)我们可以证明:若数列
3)我们可以证明:若数列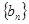 有上界(即存在常数
有上界(即存在常数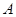 ,使得
,使得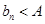 对一切
对一切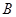 ,使得
,使得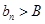 对一切
对一切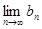 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: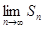 存在.
存在. 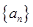 的前
的前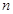 项和为
项和为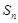 ,
,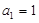 ,
,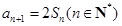 .
.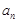 ; (Ⅱ)求数列
; (Ⅱ)求数列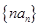 的前
的前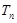 .
. 下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)

 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
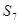 ,并归纳出
,并归纳出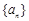 的前n项和为
的前n项和为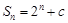 ,其中c为常数,则该数列
,其中c为常数,则该数列


