题目内容
(理)正数列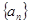 的前
的前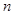 项和
项和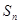 满足:
满足: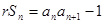 ,
,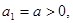 常数
常数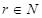
(1)求证: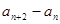 是一个定值;
是一个定值;
(2)若数列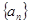 是一个周期数列,求该数列的周期;
是一个周期数列,求该数列的周期;
(3)若数列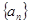 是一个有理数等差数列,求
是一个有理数等差数列,求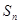 .
.
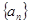 的前
的前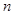 项和
项和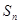 满足:
满足: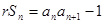 ,
,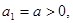 常数
常数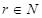
(1)求证:
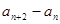 是一个定值;
是一个定值;(2)若数列
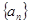 是一个周期数列,求该数列的周期;
是一个周期数列,求该数列的周期;(3)若数列
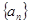 是一个有理数等差数列,求
是一个有理数等差数列,求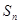 .
.(理)证明:(1)
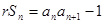 (1)
(1) 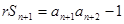 (2)
(2)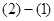 :
: 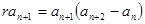 (3)
(3)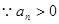
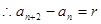 (4)
(4)……………4分
(2)计算

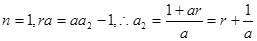 ……………6分
……………6分根据数列是隔项成等差,写出数列的前几项:
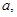
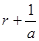 ,
,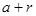 ,
,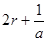 ,
,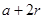 ,
,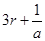 ,。。。。
,。。。。当
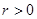 时,奇数项和偶数项都是单调递增的,所以不可能是周期数列 ……………8分
时,奇数项和偶数项都是单调递增的,所以不可能是周期数列 ……………8分所以
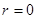 时,数列写出数列的前几项:
时,数列写出数列的前几项: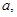
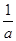 ,
,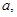
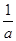 ,
,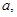
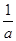 ,
,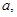
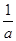 ,,。。。。
,,。。。。所以当
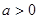 且
且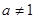 时,该数列的周期是2, ……………9分
时,该数列的周期是2, ……………9分当
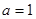 时,该数列的周期是1, ……………10分
时,该数列的周期是1, ……………10分(3)因为数列
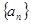 是一个有理等差数列,所以
是一个有理等差数列,所以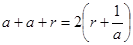
化简
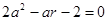 ,
,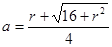 是有理数 ……………12分
是有理数 ……………12分设
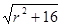 ,是一个完全平方数,设为
,是一个完全平方数,设为 ,
,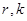 均是非负整数
均是非负整数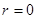 时,
时,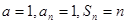 ……………14分
……………14分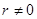 时
时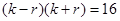 =
=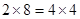 可以分解成8组,其中
可以分解成8组,其中只有
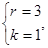 符合要求, ……………16分
符合要求, ……………16分此时
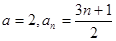
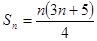 ……………18分
……………18分或者
 , ……………12分
, ……………12分等差数列的前几项:
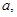
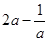 ,
,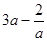 ,
,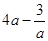 ,。。。。
,。。。。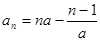 ……………14分
……………14分因为数列
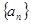 是一个有理等差数列
是一个有理等差数列 是一个自然数,
是一个自然数,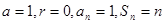 ……………16分
……………16分此时
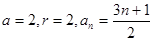
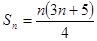 ……………18分
……………18分如果没有理由,猜想:
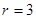 ,解答
,解答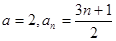
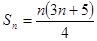 得2分
得2分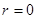
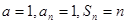 得2分
得2分略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
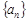 中,
中,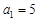 且
且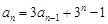 (
(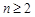 )。
)。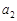 ,
,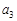 的值;
的值;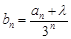 ,是否存在实数
,是否存在实数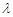 ,使数列
,使数列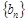 为等差数列,若存在请求其通项
为等差数列,若存在请求其通项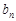 ,若不存在请说明理由。
,若不存在请说明理由。 万套,保障
万套,保障 万套(
万套( ). 预计2011年新增商品房
). 预计2011年新增商品房 万套,以后每年商品新增量是上一年新增
万套,以后每年商品新增量是上一年新增 倍,问“十二五”期间(2011年~2015年)该城市保障性住房建设年均应增加多少
倍,问“十二五”期间(2011年~2015年)该城市保障性住房建设年均应增加多少 ?
? ,
, )
) 中,对任意
中,对任意 ,
, 时都有
时都有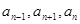 成等差,求公比
成等差,求公比 的值
的值 是等比数列
是等比数列 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出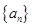 的前
的前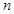 项和为
项和为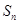 ,若对任意的
,若对任意的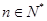 ,有
,有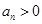 且
且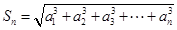 成立.
成立.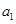 、
、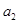 的值;
的值;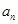 ;
;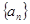 的前
的前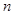 项和为
项和为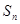 ,令
,令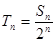 ,若对一切正整数
,若对一切正整数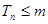 ,求
,求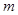 的取值范围.
的取值范围.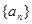 的前
的前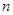 项和为
项和为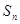 ,满足
,满足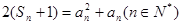 .
.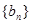 满足
满足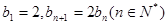 ,数列
,数列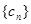 满足
满足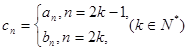 ,数列
,数列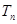 ,求
,求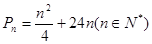 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的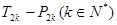 的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.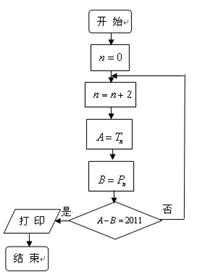
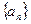 的前
的前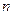 项和,
项和,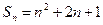 。
。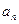 ;
;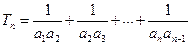 ,求
,求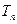 。
。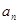 }的前n项和
}的前n项和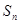 =n2,{
=n2,{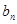 }为等比数列,且
}为等比数列,且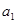 =
=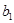 ,
,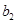 (
( -
-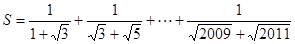 =___________
=___________