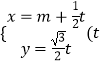题目内容
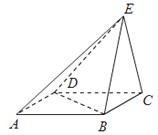
【题目】圆锥的轴截面SAB是边长为2的等边三角形，O为底面中心，M为SO的中点，动点P在圆锥底面内（包括圆周）．若AM⊥MP，则P点形成的轨迹的长度为 ．
【答案】
【解析】解：以AB所在直线为x轴，以OS为z轴，建立空间直角坐标系， 则A（﹣1，0，0），B（1，0，0）， 
， 
，设P（x，y，0）．于是有
=（1，0， 
）， 
=（x，y，﹣ ）．
由于AM⊥MP，
所以（1，0， ）（x，y，﹣ ）=0，
即x= 
，此为P点形成的轨迹方程，
其在底面圆盘内的长度为 
故答案为
建立空间直角坐标系，写出点的坐标，设出动点的坐标，利用向量的坐标公式求出向量坐标，利用向量垂直的充要条件列出方程求出动点P的轨迹方程，得到P的轨迹是底面圆的弦，利用勾股定理求出弦长．
练习册系列答案
相关题目
