题目内容
【题目】已知直线l的参数方程为 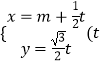 为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为
为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为 ![]() ,且直线l经过椭圆C的右焦点F.
,且直线l经过椭圆C的右焦点F.
(1)求椭圆C的内接矩形PMNQ面积的最大值;
(2)若直线l与椭圆C交于A,B两点,求|FA||FB|的值.
【答案】
(1)解:椭圆C化为5ρ2cos2θ+9ρ2sin2θ=45,∴5x2+9y2=45,
∴椭圆的标准方程: ![]() .设椭圆C的内接矩形PMNQ中,P的坐标为
.设椭圆C的内接矩形PMNQ中,P的坐标为 ![]() ,
,
∴ ![]() .
.
∴椭圆C的内接矩形PMNQ面积最大值为 ![]()
(2)解:由椭圆C的方程 ![]() ,得椭圆C的右焦点F(2,0),由直线l经过右焦点F(2,0),得m=2,
,得椭圆C的右焦点F(2,0),由直线l经过右焦点F(2,0),得m=2,
易得直线l的参数方程可化为 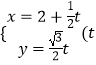 为参数),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
为参数),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
∴ ![]() ,即
,即 ![]() .
.
|FA||FB|的值 ![]()
【解析】(1)将椭圆的极坐标方程转化成标准方程,设P点坐标,根据二倍角公式及正弦函数的性质,即可求得椭圆C的内接矩形PMNQ面积的最大值;(2)将参数方程代入椭圆的标准方程,由韦达定理即可求得 ![]() ,即可求得|FA||FB|的值.
,即可求得|FA||FB|的值.

练习册系列答案
相关题目