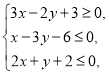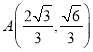题目内容
【题目】已知椭圆![]() 过点
过点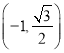 且离心率为
且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
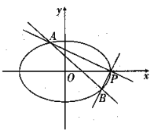
(2)如图所示,设椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() ,
,![]() 是椭圆上异于点
是椭圆上异于点![]() 的两点,直线
的两点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,试判断直线
,试判断直线![]() 是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
【答案】(1)![]() (2)是,直线
(2)是,直线![]() 过定点
过定点![]() .
.
【解析】
(1)由题意结合椭圆的性质可得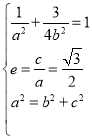 ,解出
,解出![]() ,
,![]() 后即可得解;
后即可得解;
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,联立方程可得
,联立方程可得![]() ,
,![]() ,由题意可得
,由题意可得![]() ,化简后可得
,化简后可得![]() 或
或![]() ,分别代入直线方程即可得解.
,分别代入直线方程即可得解.
(1)由题意可得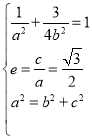 ,解得
,解得![]() ,
,![]() ,
,
则椭圆的方程为![]() .
.
(2)由题意,直线![]() 的斜率存在,
的斜率存在,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
联立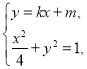 得
得![]() ,
,
![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 直线
直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
化简得![]() ,
,
![]()
![]() ,
,
化简得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() .
.
将![]() 代入
代入![]() 中,解得
中,解得![]() ,
,
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,直线过定点
,直线过定点![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,直线过定点
,直线过定点![]() ,不符合题意.
,不符合题意.
故直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目
【题目】某生物公司将A型病毒疫苗用100只小白鼠进行科研和临床试验,得到统计数据如表:
未感染病毒 | 感染病毒 | 总计 | |
未注射 | 10 | x | A |
注射 | 40 | y | B |
总计 | 50 | 50 | 100 |
现从所有试验的小白鼠中任取一只,取得注射疫苗小白鼠的概率为![]() .
.
(1)能否有99.9%的把握认为注射此型号疫苗有效?
(2)现从感染病毒的小白鼠中任取3只进行病理分析,记已注射疫苗的小白鼠只数为ξ,求ξ的分布列和数学期望.
附: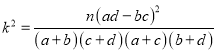
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |