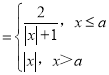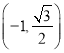Question

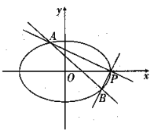
【题目】已知直线与椭圆交于两点，且（其中为坐标原点），若椭圆的离心率满足，则椭圆长轴的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

联立直线方程与椭圆方程得（a2+b2）x2﹣2a2x+a2﹣a2b2＝0，设P（x1，y1），Q（x2，y2），由OP⊥OQ，得＝0，由根与系数的关系可得：a2+b2＝2a2b2．由椭圆的离心率e满足≤e≤，化为，即可得出．

联立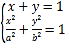 得：（a2+b2）x2﹣2a2x+a2﹣a2b2＝0，设P（x1，y1），Q（x2，y2）

△＝4a4﹣4（a2+b2）（a2﹣a2b2）＞0，化为：a2+b2＞1．

x1+x2＝ ，x1x2＝．∵OP⊥OQ，

∴＝x1x2+y1y2＝x1x2+（x1﹣1）（x2﹣1）＝2x1x2﹣（x1+x2）+1＝0，

∴2×﹣+1＝0．化为a2+b2＝2a2b2．∴b2＝．

∵椭圆的离心率e满足≤e≤，∴，∴，，化为5≤4a2≤6．

解得： ≤2a≤ ．满足△＞0．∴椭圆长轴的取值范围是[，]．

故选：A．