题目内容
18．下列函数中既是奇函数又在区间（0，+∞）上递增的是（ ）| A． | y=-3x | B． | y=2x-2-x | C． | y=x2+1 | D． | y=|x| |
分析 根据函数奇偶性和单调性的性质分别进行判断即可．
解答 解：A．y=-3x是奇函数，但在区间（0，+∞）上递减，不满足条件．
B．f（-x）=2-x-2x=-（2x-2-x）=-f（x）为奇函数，y=2x-2-x=y=2x-（$\frac{1}{2}$）x在区间（0，+∞）上递增，满足条件．
C．y=x2+1是偶函数，不满足条件．
D．y=|x|是偶函数，不满足条件．
故选：B
点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
相关题目
8．若向量$\overrightarrow{a}$=（x，3）（x∈R），则“x=4是|$\overrightarrow{a}$|=5”的（ ）
| A． | 充要条件 | B． | 必要不充分条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
9．已知双曲线C与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点F1、F2，点P为双曲线C与椭圆的一个交点，且满足|PF1|=2|PF2|，则双曲线C的渐近线方程是（ ）
| A． | y=±$\sqrt{3}$x | B． | y=±$\sqrt{2}$x | C． | y=±x | D． | y=±$\frac{\sqrt{3}}{2}$x |
6．已知具有线性相关的两个变量x，y之间的一组数据如下：
且回归方程是$\widehat{y}$=bx+a，其中b=0.95，则当x=6时，y的预测值为（ ）
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | 4.5 | 4.8 | 6.7 |
| A． | 8.1 | B． | 8.2 | C． | 8.3 | D． | 8.4 |
3．已知函数f（x）=$\left\{\begin{array}{l}{|{2}^{x}-1|（x＜1）}\\{-（x-2）^{2}+1（x≥1）}\end{array}\right.$，则关于x的方程f（x+$\frac{1}{x}$-1）=a的实根个数最多为（ ）
| A． | 5个 | B． | 6个 | C． | 7个 | D． | 8个 |
10．如图，有一个几何体的三视图及其尺寸（单位：cm），则该几何体的表面积和体积分别为（ ）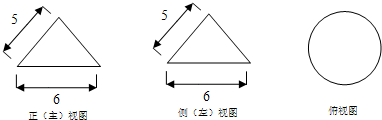
| A． | 24πcm2，12πcm3 | B． | 15πcm2，12πcm3 | C． | 24πcm2，36πcm3 | D． | 15πcm2，36πcm3 |
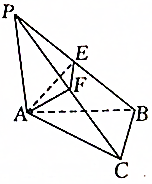如图所示，已知在△ABC中，∠C=90°，PA⊥平面ABC，AE⊥PB交PB于E，AF⊥PC于F，AP=AB=2，∠AEF=θ，当θ变化时，求三棱锥P-AEF的体积的最大值．