题目内容
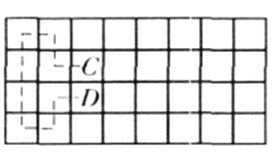
【题目】将一枚棋子放在一个![]() 的棋盘上,记
的棋盘上,记![]() 为从左、上数第
为从左、上数第![]() 行第
行第![]() 列的小方格,求所有的四元数组
列的小方格,求所有的四元数组![]() ,使得从
,使得从![]() 出发,经过每个小方格恰一次到达
出发,经过每个小方格恰一次到达![]() (每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
(每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
【答案】所求为![]() ,且当
,且当![]() 为偶数时,
为偶数时,![]() ;当
;当![]() 为奇数时,
为奇数时,![]() .
.
【解析】
将![]() 棋盘按国际象棋方式黑边相间染色,其中,
棋盘按国际象棋方式黑边相间染色,其中,![]() 为黑色,
为黑色,
当![]() 为奇数时,任两个黑色的小方格满足条件,当
为奇数时,任两个黑色的小方格满足条件,当![]() 为偶数时,任两个异色的小方格满足条件.
为偶数时,任两个异色的小方格满足条件.
记以下结论为![]() .
.
下面用数学归纳法证明,
先证下面的引理.
引理1 ![]() 与
与![]() 等价
等价
显然成立.
引理2 在![]() 棋盘中,不同列的异色的两个小方格满足条件.
棋盘中,不同列的异色的两个小方格满足条件.
引理2的证明:若![]() 同行,因二者异色,则其中间有偶数列,由如图方式知
同行,因二者异色,则其中间有偶数列,由如图方式知![]() 满足条件.
满足条件.
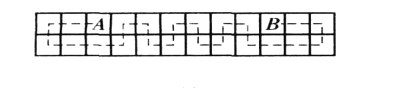
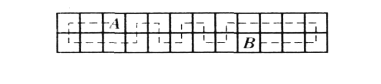
若![]() 不同行,因二者异色,则其中间有奇数列,由如图方式知
不同行,因二者异色,则其中间有奇数列,由如图方式知![]() 满足条件.
满足条件.
引理3 若![]() 成立,则
成立,则![]() 成立,
成立,
引理3的证明:对![]() 棋盘,分两种情况讨论:
棋盘,分两种情况讨论:
(1)若![]() 都不在前(后)两列,则在后(前)面的
都不在前(后)两列,则在后(前)面的![]() 棋盘中,有
棋盘中,有![]() 成立,且在前(后)第三列中必有相邻方格是
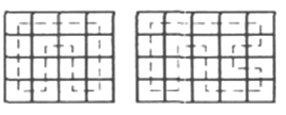
成立,且在前(后)第三列中必有相邻方格是![]() 中棋子走过的路径中连续的两个方格(设为
中棋子走过的路径中连续的两个方格(设为![]() ),可用如图
),可用如图
方式将前(后)两列并入棋子原来的路径,使![]() 成立.
成立.
(2)若![]() 一个在前两列,另一个在后两列,不妨设
一个在前两列,另一个在后两列,不妨设![]() 在前两列,则在第二列有至少两个方格与
在前两列,则在第二列有至少两个方格与![]() 异色,其中至少有一个方格(记为
异色,其中至少有一个方格(记为![]() )与
)与![]() 不同行,由引理
不同行,由引理![]() 知在前
知在前![]() 棋盘中,
棋盘中,![]() 满足条件,取第三列中与
满足条件,取第三列中与![]() 相邻的方格
相邻的方格![]() (与
(与![]() 同色),则由
同色),则由![]() 成立,知在后
成立,知在后![]() 棋盘中,
棋盘中,![]() 满足条件.
满足条件.
故由![]() ,使
,使![]() 成立.
成立.
由(1)、(2)知![]() 成立.
成立.
类似可证:
引理4 若![]() 成立,则
成立,则![]() 成立.
成立.
回到原题
由引理![]() 知,为利用数学归纳法,只需证明
知,为利用数学归纳法,只需证明![]() 成立即可.
成立即可.
对![]() 异色.
异色.
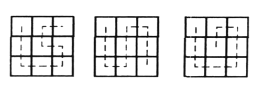
若![]() 相邻,则由如图
相邻,则由如图
环路知![]() 满足条件.
满足条件.
若![]() 不相邻,当
不相邻,当![]() 都在上(下)两行时,由引理2知在
都在上(下)两行时,由引理2知在![]() 棋盘中,
棋盘中,![]() 满足条件.
满足条件.
类似引理3
(1)知有![]() 的路径使
的路径使![]() 成立,当
成立,当![]() 一个在上两行,另一个在下两行时,类似引理3(2)知有
一个在上两行,另一个在下两行时,类似引理3(2)知有
![]() 的路径使
的路径使![]() 成立.
成立.
对![]() ,
,![]() 同黑.
同黑.
先由图知![]() 成立.
成立.
再分两种情况证![]() 成立.
成立.
若![]() 都在前(后)三列,则由
都在前(后)三列,则由![]() 成立,知在前(后)
成立,知在前(后)![]() 棋盘中,
棋盘中,![]() 满足条件,类似引理3(1)知在
满足条件,类似引理3(1)知在![]() 棋盘中有
棋盘中有![]() 路径使
路径使![]() 成立.
成立.
若![]() 一个在前两列,另一个在后两列,不妨设
一个在前两列,另一个在后两列,不妨设![]() 在前两列,由引理2知,在第2列中存在白方格
在前两列,由引理2知,在第2列中存在白方格![]() ,在第4列中存在白方格
,在第4列中存在白方格![]() ,使得分别在前、后
,使得分别在前、后![]() 棋盘中,
棋盘中,![]() 、
、![]() 分别满足条件,如图
分别满足条件,如图
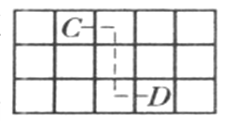
方式将![]() 、
、![]() 相连,则
相连,则![]() 使
使![]() 成立.
成立.
最后分两种情况证![]() 成立.
成立.
若![]() 都在前(后)三列,则由
都在前(后)三列,则由![]() 成立,类似引理
成立,类似引理![]() 可知在
可知在![]() 棋盘中,有
棋盘中,有![]() 路径使
路径使![]() 成立.
成立.
若![]() 一个在前两列,另一个在后两列,类似
一个在前两列,另一个在后两列,类似![]() 中第2种情况知在
中第2种情况知在![]() 棋盘中有
棋盘中有![]() 路径使
路径使![]() 成立.
成立.
故![]() 成立.
成立.
综上,所求为![]() ,且当
,且当![]() 为偶数时,
为偶数时,![]() ;
;
当![]() 为奇数时,
为奇数时,![]() .
.