题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}{3^x},x≥0\\{e^x},x<0\end{array}$,若对任意的x∈[1-3a,2a-1],不等式f[a(x+1)-x]≥[f(x)]a恒成立,则实数a的取值范围是($\frac{2}{5}$,1].分析 由1-3a<2a-1,解得a>$\frac{2}{5}$;运用指数函数的单调性,可得f(x)在R上递增,结合指数幂的运算性质,可得不等式f[a(x+1)-x]≥[f(x)]a,即为f[a(x+1)-x]≥f(ax),则有a(x+1)-x≥ax,由不等式恒成立思想即可得到a的取值范围.
解答 解:由1-3a<2a-1,解得a>$\frac{2}{5}$;
函数f(x)=$\left\{\begin{array}{l}{3^x},x≥0\\{e^x},x<0\end{array}$,
当x>0时,f(x)=3x递增,
x<0时,f(x)=ex递增.
x=0时,f(0)=1,
由函数的单调性可得f(x)在R上递增,
则有不等式f[a(x+1)-x]≥[f(x)]a,
即为f[a(x+1)-x]≥f(ax),
则有a(x+1)-x≥ax,
即为a≥x在x∈[1-3a,2a-1]上恒成立.
即有a≥2a-1,解得a≤1,
则$\frac{2}{5}$<a≤1,
故答案为:$({\frac{2}{5},1}]$.
点评 本题考查不等式的恒成立问题,主要考查函数的单调性的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
2.已知命题p:对于?x∈R,恒有2x+2-x≥2成立,命题q:奇函数f(x)的图象必过原点.则下列结论正确的是( )
| A. | p∧q为真 | B. | (?p)∨q为真 | C. | p∧(?q)为真 | D. | ?p为真 |
19.阅读如图所示的程序框图,运行相应的程序,若输入x的值为-5,则输出y的值为( )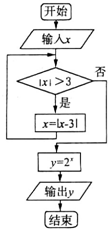

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
6.设函数f(x)=$sin(2x+\frac{π}{3})$的图象为M,下面结论中正确的是( )
| A. | 图象M可由y=sin2x的图象向左平移$\frac{π}{6}$个单位得到 | |
| B. | 函数f(x)的最小正周期是4π | |
| C. | 图象M关于直线x=$\frac{π}{3}$对称 | |
| D. | 函数y=f(x)在区间$(-\frac{5π}{6},\frac{π}{6})$上是增函数 |
3.在菱形ABCD中,∠BAD=60°,AB=4,点F是对角线BD上的动点,则$\overrightarrow{AF}$•$\overrightarrow{BF}$的最小值是( )
| A. | -3 | B. | -2 | C. | -$\frac{3}{2}$ | D. | -1 |
20.已知集合A={x|y=$\sqrt{\frac{x-1}{x-4}}$},B={y|y=$\sqrt{16-{2}^{x}}$},则A∩B=( )
| A. | [1,4] | B. | [1,4) | C. | [0,1] | D. | (0,4) |
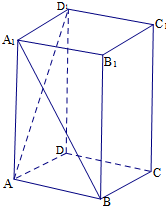
 用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?
用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?