题目内容
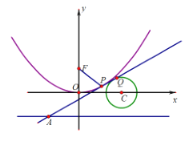
【题目】已知如图，直线
是抛物线
（
）和圆C：
的公切线，切点（在第一象限）分别为P、Q.F为抛物线的焦点，切线交抛物线的准线于A，且
.
（1）求切线的方程；
（2）求抛物线的方程.
【答案】（1）
（2）
【解析】
（1）根据抛物线定义得
，再由
可得切线的斜率，再根据圆的性质可得切点
坐标，从而得到切线
的方程.
（2）设切点
，利用导数的几何意义得出在点
的切线方程再根据（1）可求得
，代入抛物线，即可求得
，从而求得抛物线的方程.
（1）如图，过P作
准线于H.
由，知，则
.
.
设切点
，又
，则
①
又
②
由①②解得
，
，则
.
∴切线的方程为
，即.
（2）由抛物线方程
，求导数得
，
设切点，则
.
所以点P处切线方程为
，即
.
由（1）可知切线方程为，
，则
代入，得
，则
，
∴抛物线方程为.
【题目】国家学生体质健康测试专家组到某学校进行测试抽查，在高三年级随机抽取100名男生参加实心球投掷测试，测得实心球投掷距离（均在5至15米之内）的频数分布表如下（单位：米）：
分组 |
|
|
|
|
|
频数 | 9 | 23 | 40 | 22 | 6 |
规定：实心球投掷距离在
之内时，测试成绩为“良好”，以各组数据的中间值代表这组数据的平均值
，将频率视为概率.
（1）求，并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
（2）现在从实心球投掷距离在
，
之内的男生中用分层抽样的方法抽取5人，再从这5人中随机抽取3人参加提高体能的训练，求：在被抽取的3人中恰有两人的实心球投掷距离在内的概率.
【题目】某届奥运会上，中国队以26金18银26铜的成绩列金牌榜第三奖牌榜第二.某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查（结果只有“满意”和“不满意”两种），从被调查的学生中随机抽取了60人，具体的调查结果如下表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 6 | 10 | 13 | 11 | 9 | 11 |
满意人数 | 5 | 9 | 10 | 6 | 7 | 7 |
（1）在高三年级全体学生中随机抽取1名学生，由以上统计数据估计该生持满意态度的概率；
（2）若从一班和二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为
，求随机变量的分布列及数学期望.