题目内容
已知椭圆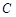 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线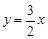 与椭圆
与椭圆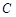 在第一象限内的交点是
在第一象限内的交点是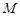 ,点
,点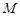 在
在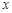 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆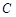 的右焦点
的右焦点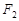 ,椭圆
,椭圆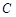 另一个焦点是
另一个焦点是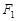 ,且
,且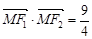
(1)求椭圆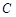 的方程;
的方程;
(2)直线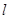 过点
过点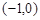 ,且与椭圆
,且与椭圆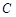 交于
交于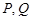 两点,求
两点,求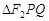 的内切圆面积的最大值
的内切圆面积的最大值
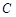 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线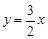 与椭圆
与椭圆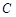 在第一象限内的交点是
在第一象限内的交点是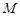 ,点
,点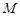 在
在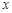 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆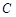 的右焦点
的右焦点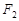 ,椭圆
,椭圆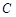 另一个焦点是
另一个焦点是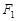 ,且
,且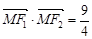
(1)求椭圆
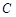 的方程;
的方程;(2)直线
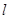 过点
过点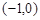 ,且与椭圆
,且与椭圆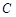 交于
交于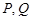 两点,求
两点,求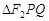 的内切圆面积的最大值
的内切圆面积的最大值(1)设椭圆方程为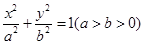 ,点
,点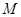 在直线
在直线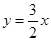 上,且点
上,且点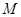 在
在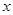 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆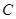 的右焦点
的右焦点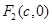 , 则点
, 则点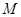 为
为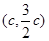
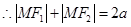 ,而
,而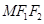 为
为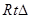 ,则有
,则有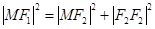
则有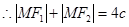 ,所以
,所以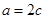
又因为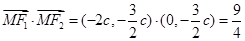
 所以
所以
所以椭圆方程为: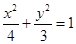 -----------------------5分
-----------------------5分
(2)由(1)知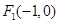 ,过点
,过点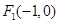 的直线与椭圆
的直线与椭圆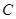 交于
交于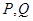 两点,则
两点,则
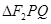 的周长为
的周长为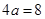 ,则
,则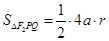 (
(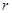 为三角形内切圆半径),当
为三角形内切圆半径),当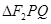 的面积最大时,其内切圆面积最大
的面积最大时,其内切圆面积最大
设直线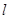 方程为:
方程为: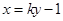 ,
,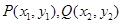 ,则
,则
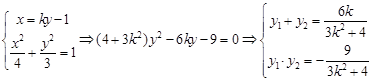
所以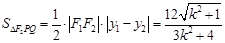
令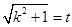 ,则
,则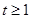 ,所以
,所以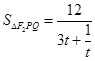 ,而
,而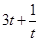 在
在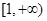 上单调递增,
上单调递增,
所以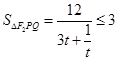 ,当
,当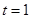 时取等号,即当
时取等号,即当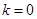 时,
时,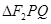 的面积最大值为3
的面积最大值为3
结合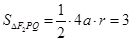 ,得
,得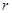 的最小值为
的最小值为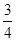
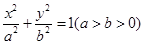 ,点
,点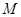 在直线
在直线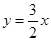 上,且点
上,且点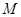 在
在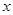 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆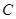 的右焦点
的右焦点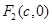 , 则点
, 则点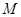 为
为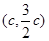
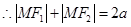 ,而
,而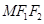 为
为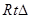 ,则有
,则有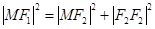
则有
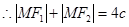 ,所以
,所以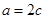
又因为
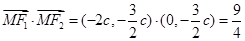
 所以
所以
所以椭圆方程为:
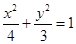 -----------------------5分
-----------------------5分(2)由(1)知
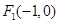 ,过点
,过点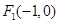 的直线与椭圆
的直线与椭圆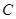 交于
交于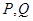 两点,则
两点,则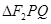 的周长为
的周长为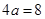 ,则
,则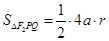 (
(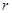 为三角形内切圆半径),当
为三角形内切圆半径),当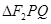 的面积最大时,其内切圆面积最大
的面积最大时,其内切圆面积最大设直线
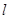 方程为:
方程为: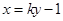 ,
,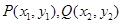 ,则
,则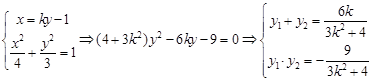
所以
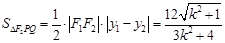
令
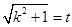 ,则
,则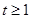 ,所以
,所以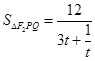 ,而
,而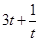 在
在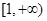 上单调递增,
上单调递增,所以
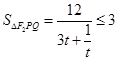 ,当
,当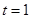 时取等号,即当
时取等号,即当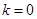 时,
时,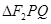 的面积最大值为3
的面积最大值为3结合
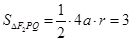 ,得
,得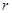 的最小值为
的最小值为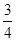
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
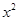 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.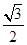 的椭圆
的椭圆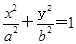 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.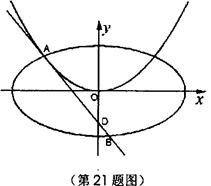
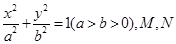 是椭圆的左、右顶点,
是椭圆的左、右顶点,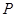 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线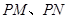 的斜率分别为
的斜率分别为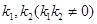 ,若
,若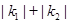 的最小值为
的最小值为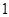 ,则椭圆的离心率为
,则椭圆的离心率为 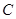 的方程为:
的方程为: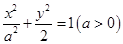 ,其焦点在
,其焦点在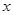 轴上,离心率
轴上,离心率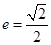 .
.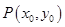 满足
满足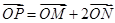 ,其中M,N是椭圆
,其中M,N是椭圆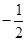 ,求证:
,求证: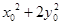 为定值.
为定值.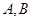 ,使得
,使得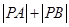 为定值?若存在,给出证明;若不存在,请说明理由.
为定值?若存在,给出证明;若不存在,请说明理由. 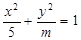 的离心率
的离心率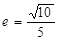 ,则
,则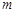 的值为:
的值为: 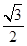 的椭圆
的椭圆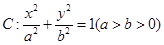 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线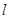 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。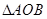 面积的最大值;
面积的最大值;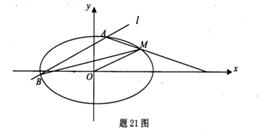
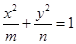 (m>n>0)和双曲线
(m>n>0)和双曲线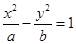 (a>b>0)有相同的焦点F1,F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是 ( )
(a>b>0)有相同的焦点F1,F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是 ( )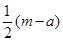
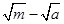
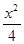 +y2=1.过点(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
+y2=1.过点(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.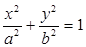 的右焦点,点P在椭圆上,△POF2是面积为
的右焦点,点P在椭圆上,△POF2是面积为 的正三角形,则b2的值是 ▲
的正三角形,则b2的值是 ▲ 