题目内容
(本小题满分12分)
如题21图,已知离心率为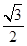 的椭圆
的椭圆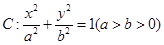 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线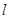 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求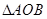 面积的最大值;
面积的最大值;
(2)证明:直线MA、MB与x轴围成一个等腰三角形。
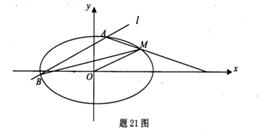
如题21图,已知离心率为
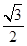 的椭圆
的椭圆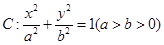 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线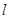 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。(1)求
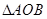 面积的最大值;
面积的最大值;(2)证明:直线MA、MB与x轴围成一个等腰三角形。

解:(Ⅰ)设椭圆
 的方程为:
的方程为: .
.由题意得:
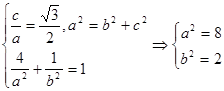
∴椭圆方程为
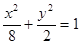 .……………3分
.……………3分由直线
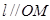 ,可设
,可设 将式子代入椭圆
将式子代入椭圆 得:
得: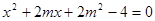
设
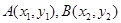 ,则
,则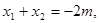
 ……………5分
……………5分由题意可得△
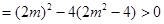 于是
于是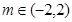 且
且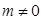
故

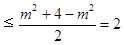 当且仅当
当且仅当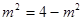 即
即 时,
时,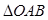 面积的最大值为
面积的最大值为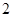 .
.……………7分
(Ⅱ)设直线
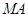 、
、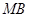 的斜率分别为
的斜率分别为 、
、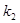 ,
,则
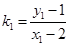
 ……………9分
……………9分下面只需证明:
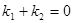 ,事实上,
,事实上,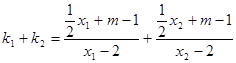
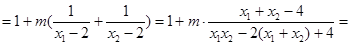

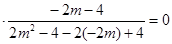
故直线
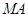 、
、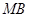 与
与 轴围成一个等腰三角形.……………12分
轴围成一个等腰三角形.……………12分略

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
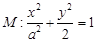
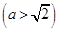 的右焦点为
的右焦点为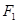 ,直线
,直线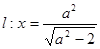 与
与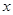 轴交于点
轴交于点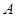 ,若
,若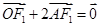 (其中
(其中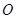 为坐标原点).
为坐标原点).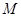
 的方程;
的方程;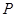 是椭圆
是椭圆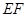 为圆
为圆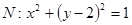 的任意一条直径(
的任意一条直径(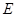 ,
,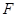 为直径的两个端点),求
为直径的两个端点),求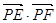 的最大值.
的最大值.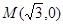 ,椭圆
,椭圆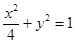 与直线
与直线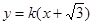 交于点
交于点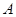 、
、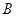 ,则
,则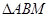 的周长为( )
的周长为( )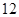
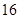
 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线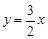 与椭圆
与椭圆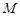 ,点
,点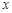 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆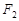 ,椭圆
,椭圆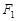 ,且
,且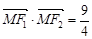
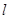 过点
过点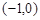 ,且与椭圆
,且与椭圆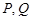 两点,求
两点,求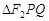 的内切圆面积的最大值
的内切圆面积的最大值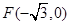 ,右顶点为
,右顶点为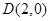 ,设点
,设点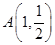 .
.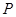 是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点
是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点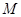 的轨迹方程;
的轨迹方程;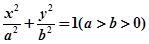 的右焦点的弦为直径的圆与直线
的右焦点的弦为直径的圆与直线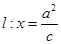 的位置关系是
的位置关系是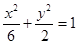 和双曲线
和双曲线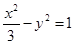 有公共焦点为
有公共焦点为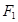 、
、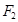 ,
,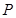 是两曲线的一个公共点,则
是两曲线的一个公共点,则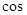 ∠
∠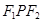 ( )
( )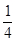

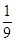

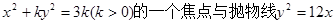 的焦点重合,则该椭圆的离心率是 .
的焦点重合,则该椭圆的离心率是 .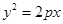 的焦点与椭圆
的焦点与椭圆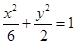 的右焦点重合,则
的右焦点重合,则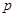 的值为______.
的值为______.