题目内容
(本小题满分14分)已知椭圆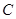 的方程为:
的方程为: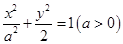 ,其焦点在
,其焦点在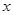 轴上,离心率
轴上,离心率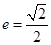 .
.
(1)求该椭圆的标准方程;
(2)设动点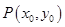 满足
满足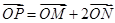 ,其中M,N是椭圆
,其中M,N是椭圆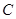 上的点,直线OM与ON的斜率之积为
上的点,直线OM与ON的斜率之积为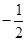 ,求证:
,求证: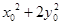 为定值.
为定值.
(3)在(2)的条件下,问:是否存在两个定点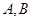 ,使得
,使得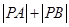 为定值?若存在,给出证明;若不存在,请说明理由.
为定值?若存在,给出证明;若不存在,请说明理由.
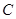 的方程为:
的方程为: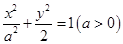 ,其焦点在
,其焦点在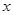 轴上,离心率
轴上,离心率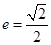 .
.(1)求该椭圆的标准方程;
(2)设动点
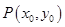 满足
满足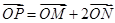 ,其中M,N是椭圆
,其中M,N是椭圆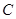 上的点,直线OM与ON的斜率之积为
上的点,直线OM与ON的斜率之积为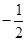 ,求证:
,求证: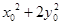 为定值.
为定值.(3)在(2)的条件下,问:是否存在两个定点
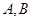 ,使得
,使得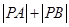 为定值?若存在,给出证明;若不存在,请说明理由.
为定值?若存在,给出证明;若不存在,请说明理由. 解:(1)由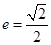 ,
, ,解得
,解得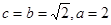 ,
,
故椭圆的标准方程为 . ……………………3分
. ……………………3分
(2)设 ,
,
则由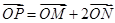 ,得
,得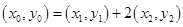 ,
,
即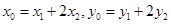 ,
,
∵点M,N在椭圆 上,∴
上,∴ ……6分
……6分
设 分别为直线
分别为直线 的斜率,由题意知,
的斜率,由题意知,
 ,∴
,∴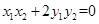 , ……………………8分
, ……………………8分
故
 ,
,
即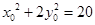 (定值) ……………………10分
(定值) ……………………10分
(3)由(2)知点 是椭圆
是椭圆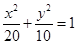 上的点,
上的点,
∵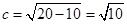 ,
,
∴该椭圆的左右焦点 满足
满足 为定值,
为定值,
因此存在两个定点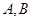 ,使得
,使得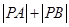 为定值。 …………………14分
为定值。 …………………14分
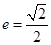 ,
, ,解得
,解得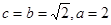 ,
,故椭圆的标准方程为
 . ……………………3分
. ……………………3分(2)设
 ,
,则由
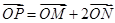 ,得
,得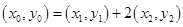 ,
,即
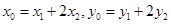 ,
,∵点M,N在椭圆
 上,∴
上,∴ ……6分
……6分设
 分别为直线
分别为直线 的斜率,由题意知,
的斜率,由题意知, ,∴
,∴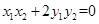 , ……………………8分
, ……………………8分故

 ,
,即
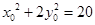 (定值) ……………………10分
(定值) ……………………10分(3)由(2)知点
 是椭圆
是椭圆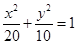 上的点,
上的点,∵
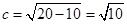 ,
,∴该椭圆的左右焦点
 满足
满足 为定值,
为定值,因此存在两个定点
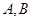 ,使得
,使得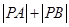 为定值。 …………………14分
为定值。 …………………14分略

练习册系列答案
相关题目
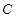 的方程为
的方程为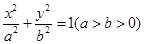 ,称圆心在坐标原点
,称圆心在坐标原点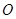 ,半径为
,半径为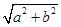 的圆为椭圆
的圆为椭圆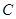 的“伴随圆”,椭圆
的“伴随圆”,椭圆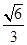 .
.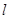 与椭圆
与椭圆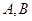 两点,与其“伴随圆”交于
两点,与其“伴随圆”交于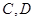 两点,当
两点,当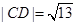 时,求△
时,求△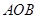 面积的最大值.
面积的最大值.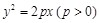 的焦点F恰好是椭圆
的焦点F恰好是椭圆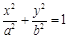 的右焦点,且两条曲线交点的连线过点F,则该椭圆的离心率为____________.
的右焦点,且两条曲线交点的连线过点F,则该椭圆的离心率为____________.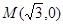 ,椭圆
,椭圆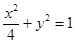 与直线
与直线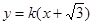 交于点
交于点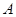 、
、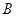 ,则
,则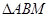 的周长为( )
的周长为( )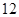
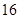
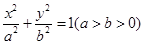 与双曲线
与双曲线 有共同的焦点,
有共同的焦点,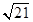

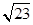
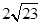
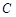 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线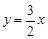 与椭圆
与椭圆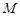 ,点
,点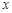 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆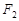 ,椭圆
,椭圆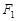 ,且
,且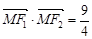
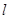 过点
过点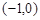 ,且与椭圆
,且与椭圆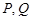 两点,求
两点,求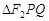 的内切圆面积的最大值
的内切圆面积的最大值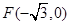 ,右顶点为
,右顶点为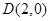 ,设点
,设点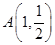 .
.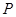 是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点
是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点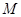 的轨迹方程;
的轨迹方程;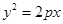 的焦点与椭圆
的焦点与椭圆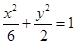 的右焦点重合,则
的右焦点重合,则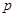 的值为______.
的值为______.