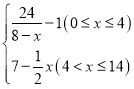题目内容
【题目】如图，已知底角为
的等腰梯形
，底边
长为12，腰长为
，当一条垂直于底边
(垂足为
）的直线
从左至右移动（与梯形
有公共点）时，直线
把梯形分成两部分.
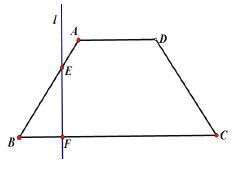
（1）令
，试写出直线右边部分的面积
与
的函数解析式；
（2）在（1）的条件下，令
.构造函数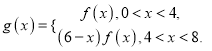
①判断函数
在
上的单调性；
②判断函数
在定义域内是否具有单调性，并说明理由.
【答案】（1）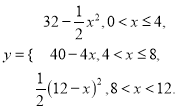
；（2）见解析.
【解析】试题分析：首先根据题意寻求y 与自变量x的关系，根据x的不同情况求出y与x的函数关系，得出分段函数；根据所求出的函数f(x)的解析式，按照函数g(x)的要求，写出对应的函数g(x)的解析式，研究函数g(x)在（4，8）的单调性，按照分段函数的解析式分段研究函数的单调性.
试题解析：
（1）过点
分别作
，垂足分别是
.因为等腰梯形
的底角为
，腰长为
，所以
,又
，所以
.
当点
在
上时，即
时， 
；
当点
在
上时，即
时， 
；
当点
在
上时，即
时， 
.
所以，函数解析式为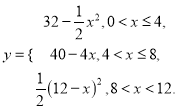
（2）
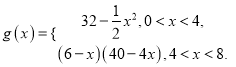
① 由二次函数的性质可知，函数
在
上是减函数.
② 虽然
在
和
单调递减，
但是
，∴
.
因此函数
在定义域内不具有单调性.
练习册系列答案
阅读快车系列答案
相关题目
【题目】网络购物已经成为一种时尚，电商们为了提升知名度，加大了在媒体上的广告投入．经统计，近五年某电商在媒体上的广告投入费用x（亿元）与当年度该电商的销售收入y（亿元）的数据如下表：）：
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
（1）求y关于x的回归方程； （2）2017年度该电商准备投入广告费1.5亿元，
利用（1）中的回归方程，预测该电商2017年的销售收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：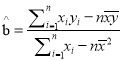 
，选用数据： 
， 
