题目内容
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
【答案】(1)当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;(2)当点D为AB中点或与点B重合时,堤坝最长
;(2)当点D为AB中点或与点B重合时,堤坝最长![]() .
.
【解析】试题分析:
利用题意求得堤坝长的函数解析式结合导函数研究函数的性质可得当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;当点D为AB中点或与点B重合时,堤坝最长
;当点D为AB中点或与点B重合时,堤坝最长![]() .
.
试题解析:
设AD为![]() 米,则
米,则![]() .
.
![]()
![]() ,
,
由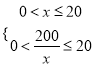 得,
得, ![]() .
.
![]() .
.
令![]() ,
, ![]() ,则
,则![]() ,
,
![]() ,
,
令![]() 得,
得, ![]() ,
, ![]() 得,
得, ![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ;
; ![]() ,
,
∴当AD为![]() 时,堤坝最短
时,堤坝最短![]() ;
;
当点D为AB中点或与点B重合时,堤坝最长![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.