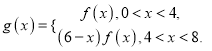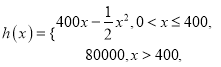Question

【题目】已知函数的定义域是.

（1）判断在上的单调性，并证明；

（2）若不等式对任意恒成立，求实数的取值范围.

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：首先要注意到大家熟知的常用的函数，第一定义域为R，第二这个函数是奇函数，第三它是单增函数，熟悉这3条，本题的第一步就只需按定义去证明了，有了函数的单调性，利用函数的单调性与奇偶性解不等式，利用极值原理求出参数的取值范围.

试题解析：

（1）因为函数的定义域为，对于函数定义域内的每一个，都有

所以，函数是奇函数.

设是上任意两个实数，且，则

.

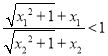由，得， 即.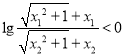

于是，

即.

所以函数在上是増函数，且

易证函数在上是増函数，且.

∵

∴函数在上是増函数.

（2） 等价于，即

原条件等价于对任意恒成立，

只需要.

令，设函数.

由函数的单调性可知.

∴

∴实数的取值范围.