题目内容
【题目】已知椭圆![]() (
(![]() 为参数),存在一条直线,使得此直线被这些椭圆截得的线段长都等于
为参数),存在一条直线,使得此直线被这些椭圆截得的线段长都等于![]() ,求直线方程_____.
,求直线方程_____.
【答案】![]()
【解析】
先判断出椭圆![]() (
(![]() 为参数)表示中心在直线
为参数)表示中心在直线![]() 上,长轴长和短轴长分别为4,2的一组椭圆,判断出符合条件的直线需要与直线
上,长轴长和短轴长分别为4,2的一组椭圆,判断出符合条件的直线需要与直线![]() 平行,设出直线方程,先利用一个特殊的椭圆与直线方程联立求出直线的方程,再证明对于所有的椭圆都满足条件.
平行,设出直线方程,先利用一个特殊的椭圆与直线方程联立求出直线的方程,再证明对于所有的椭圆都满足条件.
解:椭圆![]() (
(![]() 为参数)可化为
为参数)可化为![]() ,
,
所以![]() 表示中心在直线
表示中心在直线![]() 上,长轴长和短轴长分别为4,2的一组椭圆,而所求的直线与这组椭圆种的任意椭圆都相交,
上,长轴长和短轴长分别为4,2的一组椭圆,而所求的直线与这组椭圆种的任意椭圆都相交,
若所求的直线![]() 与直线
与直线![]() 不平行,则必定存在椭圆与直线
不平行,则必定存在椭圆与直线![]() 不相交,
不相交,
于是,设所求直线的方程为![]() ,
,
因为此直线被这些椭圆截得的线段长都等于![]() ,则直线
,则直线![]() 与椭圆
与椭圆![]() 所得到弦长为
所得到弦长为![]() ,设弦的两端点为
,设弦的两端点为![]() ,
,![]() ,
,
由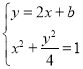 得
得![]() ,所以
,所以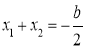 ,
,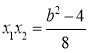 ,
,
所以![]() ,即
,即![]() ,
,
解得![]() ,
,
设直线![]() 与椭圆
与椭圆![]() (
(![]() 为参数),相交所得的弦长为
为参数),相交所得的弦长为![]() ,弦的两端点为:
,弦的两端点为:![]() ,
,![]() ,
,
则由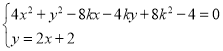 得
得![]() ,
,
所以![]() ,
,![]() ,
,
因此![]()
所以直线![]() 与椭圆
与椭圆![]() (
(![]() 为参数)相交所得的弦长为
为参数)相交所得的弦长为![]() .
.
同理可证,对任意![]() ,椭圆
,椭圆![]() (
(![]() 为参数)与直线
为参数)与直线![]() 相交所得弦长为
相交所得弦长为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目