题目内容
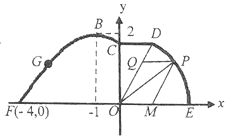
【题目】在平面直角坐标系![]() 中,已知抛物线C:
中,已知抛物线C:![]() (
(![]() )的焦点F在直线
)的焦点F在直线![]() 上,平行于x轴的两条直线
上,平行于x轴的两条直线![]() ,
,![]() 分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.
分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.

(1)求抛物线C的方程;
(2)若F在线段![]() 上,P是
上,P是![]() 的中点,证明:
的中点,证明:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据抛物线的焦点在直线![]() 上,可求得
上,可求得![]() 的值,从而求得抛物线的方程;
的值,从而求得抛物线的方程;
(2)法一:设直线![]() ,
,![]() 的方程分别为
的方程分别为![]() 和
和![]() 且
且![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,进而可得直线
的坐标,进而可得直线![]() 的方程,根据
的方程,根据![]() 在直线
在直线![]() 上,可得
上,可得![]() ,再分别求得
,再分别求得![]() ,
,![]() ,即可得证;法二:设
,即可得证;法二:设![]() ,
,![]() ,则
,则![]() ,根据直线
,根据直线![]() 的斜率不为0,设出直线
的斜率不为0,设出直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 和抛物线
和抛物线![]() 的方程,结合韦达定理,分别求出
的方程,结合韦达定理,分别求出![]() ,
,![]() ,化简
,化简![]() ,即可得证.
,即可得证.
(1)抛物线C的焦点![]() 坐标为
坐标为![]() ,且该点在直线
,且该点在直线![]() 上,
上,
所以![]() ,解得
,解得![]() ,故所求抛物线C的方程为
,故所求抛物线C的方程为![]()
(2)法一:由点F在线段![]() 上,可设直线
上,可设直线![]() ,
,![]() 的方程分别为
的方程分别为![]() 和
和![]() 且
且![]() ,
,![]() ,
,![]() ,则
,则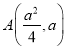 ,
,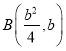 ,
,![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为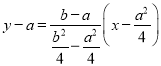 ,即
,即![]() .
.
又点![]() 在线段
在线段![]() 上,∴
上,∴![]() .
.
∵P是![]() 的中点,∴
的中点,∴![]()
∴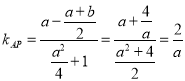 ,
,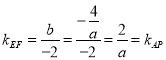 .
.
由于![]() ,
,![]() 不重合,所以
不重合,所以![]()
法二:设![]() ,
,![]() ,则
,则![]()
当直线![]() 的斜率为0时,不符合题意,故可设直线
的斜率为0时,不符合题意,故可设直线![]() 的方程为
的方程为![]()
联立直线![]() 和抛物线
和抛物线![]() 的方程
的方程![]() ,得
,得![]()
又![]() ,
,![]() 为该方程两根,所以
为该方程两根,所以![]() ,
,![]() ,
, ,
,![]() .
.
 ,
,![]()
由于![]() ,
,![]() 不重合,所以
不重合,所以![]()

【题目】为了了解居民的家庭收入情况,某社区组织工作人员从该社区的居民中随机抽取了100户家庭进行问卷调查.经调查发现,这些家庭的月收入在3000元到10000元之间,根据统计数据作出如图所示的频率分布直方图:
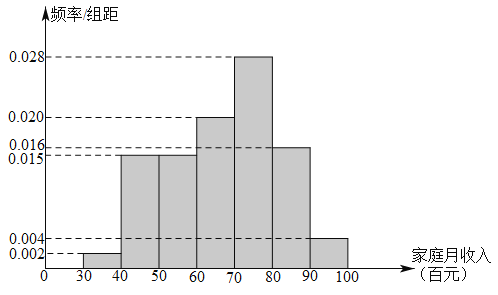
(1)经统计发现,该社区居民的家庭月收入![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.若
近似为样本平均数.若![]() 落在区间
落在区间![]() 的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区
的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区![]() 家庭月收入为4100元,试判断
家庭月收入为4100元,试判断![]() 家庭是否属于“收入较低家庭”,并说明原因;
家庭是否属于“收入较低家庭”,并说明原因;
(2)将样本的频率视为总体的概率.
①从该社区所有家庭中随机抽取![]() 户家庭,若这
户家庭,若这![]() 户家庭月收入均低于8000元的概率不小于50%,求
户家庭月收入均低于8000元的概率不小于50%,求![]() 的最大值;
的最大值;
②在①的条件下,某生活超市赞助了该社区的这次调查活动,并为这次参与调查的家庭制定了赠送购物卡的活动,赠送方式为:家庭月收入低于![]() 的获赠两次随机购物卡,家庭月收入不低于
的获赠两次随机购物卡,家庭月收入不低于![]() 的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
赠送购物卡金额(单位:元) | 100 | 200 | 300 |
概率 |
|
|
|
则![]() 家庭预期获得的购物卡金额为多少元?(结果保留整数)
家庭预期获得的购物卡金额为多少元?(结果保留整数)