题目内容
【题目】如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是 . (填序号)
①MB∥平面A1DE;
②|BM|是定值;
③A1C⊥DE.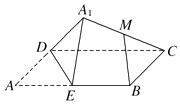
【答案】①②
【解析】解:取CD中点F,连接MF,BF,则MF∥DA1 , BF∥DE,
∴平面MBF∥平面A1DE,
∴MB∥平面A1DE,
故①正确.
由∠A1DE=∠MNB,MN= ![]() A1D=定值,NB=DE=定值,
A1D=定值,NB=DE=定值,
由余弦定理可得MB2=MN2+NB2﹣2MNNBcos∠MNB,
所以MB是定值,故②正确.
∵A1C在平面ABCD中的射影为AC,AC与DE不垂直,
∴故③不正确.
所以答案是:①②.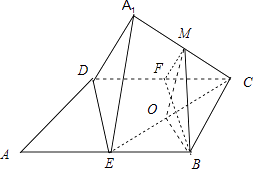
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目
