题目内容
20.已知P={x|x2-$\frac{3}{2}$x+$\frac{1}{2}$≤0},S={x|x2-(2a+1)x+a(a+1)≤0}(1)否存在实数a,使x∈P是x∈S的充要条件,若存在,求出a的范围;
(2)是否存在实数a,使x∈P是x∈S的必要不充分条件,若存在,求出a的范围.
分析 先求出关于p,q的x的范围,结合充分必要条件的定义判断即可.
解答 解:(1)∵P={x|x2-$\frac{3}{2}$x+$\frac{1}{2}$≤0}={x|$\frac{1}{2}$≤x≤1},
S={x|x2-(2a+1)x+a(a+1)≤0}={x|a≤x≤a+1},
若x∈P是x∈S的充要条件,则$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{a+1=1}\end{array}\right.$,无解,
故不存在a满足条件;
(2)若x∈P是x∈S的必要不充分条件,则$\left\{\begin{array}{l}{a≥\frac{1}{2}}\\{a+1≤1}\end{array}\right.$,无解,
故不存在a满足条件.
点评 本题考查了充分必要条件,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
5.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+4a,x<1\\-x+1,x≥1\end{array}$是定义在R上的减函数,则a的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |
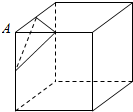 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论: