题目内容
11.下列命题:①函数f(x)=loga(2x-1)-1的图象过定点(1,-1);
②定义在R上的奇函数f(x)必满足f(0)=0;
③A=R,B=R,$f:x→y=\frac{1}{x+1}$,则f为A到B的映射;
④在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.
其中真命题的序号是①②④(把你认为正确的命题的序号都填上).
分析 根据对数函数的图象和性质,可判断①;根据奇函数的性质,可判断②;根据映射的与定义,可判断③;根据指数函数的图象和性质,可判断④.
解答 解:对于①,当x=-1时,loga(2x-1)-1=-1恒成立,故函数f(x)=loga(2x-1)-1的图象过定点(1,-1),故①正确;
对于②,定义在R上的奇函数f(x),f(0)=-f(0)=0,故②正确;
对于③,A=R,B=R,$f:x→y=\frac{1}{x+1}$,则A中元素-1在B中没有对应的元素,故f不是A到B的映射,故③错误;
对于④,在同一坐标系中,y=2x与y=$(\frac{1}{2})^{2}$=2-x的图象关于y轴对称,故④正确.
故真命题的序号是:①②④,
故答案为:①②④.
点评 本题考查的知识点是命题的真假判断与应用,函数的图象和性质,难度中档.

练习册系列答案
相关题目
10.已知$\overrightarrow{a}$=(m-1,1),$\overrightarrow{b}$=(-n-1,2),其中m>0,n>0,若存在实数λ使$\overrightarrow{b}=λ\overrightarrow{a}$,则$\frac{1}{m}$+$\frac{2}{n}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
20.已知函数y=$\frac{{\sqrt{1-x}}}{{{x^2}-4}}$,其定义域为( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-2)∪(-2,1] | D. | [1,2)∪(2,+∞) |
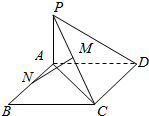 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.