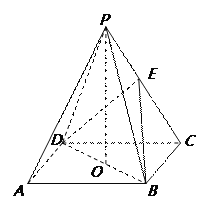
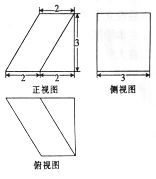
题目内容
【题目】已知函数![]() 为奇函数,且x=-1处取得极大 值2.
为奇函数,且x=-1处取得极大 值2.
(1)求f(x)的解析式;
(2)过点A(1,t) ![]() 可作函数f(x)图像的三条切线,求实数t的取值范围;
可作函数f(x)图像的三条切线,求实数t的取值范围;
(3)若![]() 对于任意的
对于任意的![]() 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
【答案】(1)![]() (2)(-3,-2) (3)
(2)(-3,-2) (3)![]()
【解析】试题分析:(1)由已知得 ,由此能求出
,由此能求出![]() 解析式.
解析式.
(2)设切点为![]() ,则
,则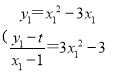 ,消去
,消去![]() 得
得![]() 设
设![]() ,由此利用导数性质能求出实数
,由此利用导数性质能求出实数![]() 的取值范围).
的取值范围).
(3)由已知得![]() 由此利用构造法和导数性质能求出实数m的取值范围.
由此利用构造法和导数性质能求出实数m的取值范围.
试题解析:
(1)因为f(x)为奇函数,故b=d=0
又![]() ,故-a-c=2,3a+c=0,解得a=1,x=-3,故
,故-a-c=2,3a+c=0,解得a=1,x=-3,故![]()
(2)设切点为![]() ,则
,则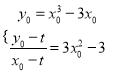 ,消去
,消去![]() 得,
得, ![]()
设![]() ,则
,则![]() ,所以g(x)在
,所以g(x)在![]() 上递减,在(0,1)上递增,所以g(x)的极大值为g(1)=-2,极小值为g(0)=-3
上递减,在(0,1)上递增,所以g(x)的极大值为g(1)=-2,极小值为g(0)=-3
因为过A的切线有三条,所以实数t的取值范围是(-3,-2)
(3)依题意, ![]() 在
在![]() 上恒成立
上恒成立
当x=0时, ![]() ;
;
当x>0时,则须![]() 在
在![]() 上恒成立
上恒成立
令![]() 则
则![]()
故![]()
所以![]()

【题目】莫言是中国首位获得诺贝尔文学奖的文学家,国人欢欣鼓舞。某高校文学社从男女生中各抽取50名同学调查对莫言作品的了程度,结果如下:
阅读过莫言的作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
(1)试估计该学校学生阅读莫言作品超过50篇的概率.
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”,根据题意完成下表,并判断能否有![]() 的把握认为“对莫言作品的非常了解”与性别有关?
的把握认为“对莫言作品的非常了解”与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
注:K2=
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
【题目】宁夏某市2008年至2012年新建商品住宅每平方米的均价![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
年份序号x | 1 | 2 | 3 | 4 | 5 |
每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
(Ⅰ)求y关于x的线性回归方程![]() ;
;
(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为
 ,
, ![]()
【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据:![]() ,
,![]() )
)