题目内容
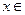
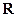 时,一次函数
时,一次函数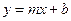 在
在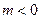 和
和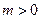 时的单调性是怎样的?利用函数单调性的定义证明你的结论.
时的单调性是怎样的?利用函数单调性的定义证明你的结论.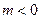 时,
时,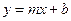 是
是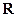 上的减函数,
上的减函数,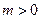 时,
时,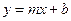 是
是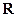 上的增函数.
上的增函数.任取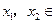
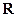 ,且
,且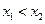 则
则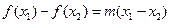 ,
,
由题设有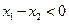 ,当
,当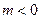 时,
时,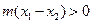 ,所以
,所以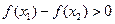 .
.
于是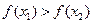 ,所以
,所以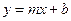 是
是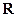 上的减函数.
上的减函数.
同理可证,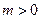 时,
时,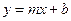 是
是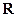 上的增函数.
上的增函数.
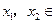
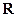 ,且
,且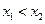 则
则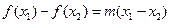 ,
,由题设有
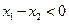 ,当
,当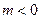 时,
时,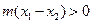 ,所以
,所以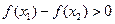 .
.于是
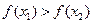 ,所以
,所以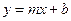 是
是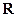 上的减函数.
上的减函数.同理可证,
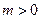 时,
时,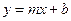 是
是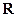 上的增函数.
上的增函数.
练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
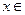
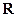 时,一次函数
时,一次函数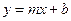 在
在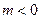 和
和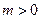 时的单调性是怎样的?利用函数单调性的定义证明你的结论.
时的单调性是怎样的?利用函数单调性的定义证明你的结论.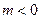 时,
时,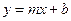 是
是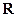 上的减函数,
上的减函数,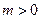 时,
时,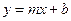 是
是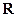 上的增函数.
上的增函数.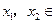
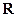 ,且
,且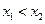 则
则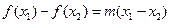 ,
,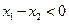 ,当
,当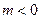 时,
时,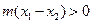 ,所以
,所以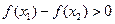 .
.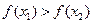 ,所以
,所以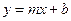 是
是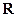 上的减函数.
上的减函数.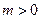 时,
时,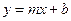 是
是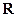 上的增函数.
上的增函数.
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案