题目内容
15.某师范大学地理学院决定从n位优秀毕业生(包括x位女学生,3位男学生)中选派2位学生到某贫困山区的一所中学担任第三批顶岗实习教师,每一位学生被选派的机会是相同的.(1)若选派的2位学生中恰有1位女学生的概率为$\frac{3}{5}$,试求出n与x的值;
(2)在(1)的条件下,记X为选派的2位学生中女学生的人数,写出X的分布列.
分析 (1)分类判断总方法:${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,2位学生中恰有1位女学生的方法数为C${\;}_{n-3}^{1}$C${\;}_{3}^{1}$,运用概率公式求解n即可.判断得出两种类型$\left\{\begin{array}{l}{n=5}\\{x=2}\end{array}\right.$或$\left\{\begin{array}{l}{n=6}\\{x=3}\end{array}\right.$,
(2)X为选派的2位学生中女学生的人数,得出X可能的取值为0,1,2,分别求解概率,列出分布列即可.
解答 解:(1)若选派的2位学生中恰有1位女学生的概率为$\frac{3}{5}$,而从n位优秀毕业生中选派2位学生担任第三批顶岗实习教师的总方法:${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,2位学生中恰有1位女学生的方法数为C${\;}_{n-3}^{1}$C${\;}_{3}^{1}$=(n-3)×3.
依题意可得:$\frac{3(n-3)}{\frac{n(n-1)}{2}}$=$\frac{3}{5}$,
化简得n2-11n+30=0,解得n1=5,n2=6.
当n=5时,x=5-3=2;当n=6时,x=6-3=3.
故(2)当$\left\{\begin{array}{l}{n=5}\\{x=2}\end{array}\right.$时,X可能的取值为0,1,2,
X=0表示只选派2位男生,这时P(X=0)=$\frac{{{C}_{2}^{0}C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$,
X=1表示选派1位男生与1位女生,这时P(X=1)=$\frac{{{C}_{2}^{1}C}_{3}^{1}}{{C}_{5}^{2}}$=$\frac{3}{5}$,
X=2表示只选派2位女生,这时P(X=2)=$\frac{{{C}_{2}^{2}C}_{3}^{0}}{{C}_{5}^{2}}$=$\frac{1}{10}$.
X的分布列为
| X | 0 | 1 | 2 |
| P | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
X=1表示选派1位男生与1位女生,这时P(X=1)=$\frac{{{C}_{3}^{1}C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$,
X=2表示只选派2位女生,这时P(X=2)=$\frac{{{C}_{3}^{0}C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$.
X的分布列为
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考察了概率在实际问题中的应用,分类讨论,考察了学生的阅读能力,计算化简能力,属于中档题.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处就没有切线 | |
| B. | 若曲线y=f(x)在点(x0,y0)处有切线,则f′(x0)必存在 | |
| C. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处的切线斜率不存在 | |
| D. | 若曲线y=f(x)在点(x0,y0)处没有切线,则f′(x0)有可能存在 |
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
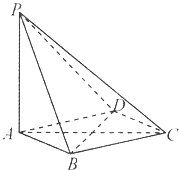 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.