题目内容
5.圆锥底面半径为3,母线长为12,B是母线PA的中点,则点A绕圆锥一周到达点B的最短距离为$6\sqrt{5}$.分析 首先将点A绕圆锥一周到达点B的距离转化为圆锥的展开图中两点之间的距离问题解答.
解答 解:圆锥的展开图为扇形,扇形的圆心角为$\frac{2π×3}{12}=\frac{π}{2}$,母线长为12,B是母线PA的中点,则点A绕圆锥一周到达点B的最短距离为展开图中AB=$\sqrt{P{A}^{2}+P{B}^{2}}$=$\sqrt{1{2}^{2}+{6}^{2}}$=$6\sqrt{5}$;
故答案为:6$\sqrt{5}$.
点评 本题考查了圆锥的侧面中两点之间的距离问题;关键是转化为平面内两点之间线段最短解答.用到了勾股定理求长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知${a_n}=\frac{1}{n-50.5}$(n∈N*),数列{an}的前项和为Sn,则使Sn>0的n最小值是( )
| A. | 99 | B. | 100 | C. | 101 | D. | 102 |
17.下列说法正确的是( )
| A. | 反证法是逆推法 | B. | 合情推理得到的结论都是正确的 | ||
| C. | 演绎推理可以作为证明的步骤 | D. | 分析法是间接证法 |
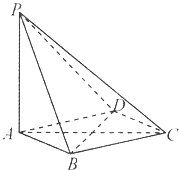 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.