题目内容
6.设a∈R,f(x)=cosx(asinx-cosx)+cos2($\frac{π}{2}$-x),且满足f(-$\frac{π}{3}$)=f(0).(1)求函数f(x)的最小正周期,对称中心;
(2)求函数f(x)在[-π,π]上的单调递增区间.
分析 (1)利用二倍角公式化简函数f(x),然后f(-$\frac{π}{3}$)=f(0),求出a的值,进一步化简为f(x)=2sin(2x-$\frac{π}{6}$),由正弦函数的图象和性质即可求得最小正周期,对称中心;
(2)求出函数在定义域上的单调递增区间,结合x的范围即可得解.
解答 解:(1)f(x)=cosx(asinx-cosx)+cos2($\frac{π}{2}$-x)
=asinxcosx-cos2x+sin2x
=$\frac{a}{2}$sin2x-cos2x
由f(-$\frac{π}{3}$)=f(0)得-$\frac{\sqrt{3}}{2}$•$\frac{a}{2}$+$\frac{1}{2}$=-1
解得a=2$\sqrt{3}$,所以f(x)=2sin(2x-$\frac{π}{6}$),
所以,函数f(x)的最小正周期T=$\frac{2π}{2}=π$,由2x-$\frac{π}{6}$=kπ,k∈Z可解得对称中心为:($\frac{kπ}{2}+\frac{π}{12}$,0)k∈Z.
(2)由2k$π-\frac{π}{2}$≤2x-$\frac{π}{6}$≤2k$π+\frac{π}{2}$,k∈Z可解得在定义域上的单调递增区间为:x∈[k$π-\frac{π}{6}$,k$π+\frac{π}{3}$],k∈Z,
∵x∈[-π,π],
∴x∈[-π,-$\frac{2π}{3}$]时,2x-$\frac{π}{6}$∈[-$\frac{13π}{6}$,-$\frac{3π}{2}$],f(x)是增函数,
x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,2x-$\frac{π}{6}$∈[-$\frac{π}{2}$,$\frac{π}{2}$],f(x)是增函数,
x∈[$\frac{5π}{6}$,π]时,2x-$\frac{π}{6}$∈[$\frac{3π}{2}$,$\frac{11π}{6}$],f(x)是增函数,
∴函数f(x)在[-π,π]上的单调递增区间为:[-π,-$\frac{2π}{3}$]∪[-$\frac{π}{6}$,$\frac{π}{3}$]∪[$\frac{5π}{6}$,π].
点评 本题主要考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,是常考题型,属于中档题.

 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.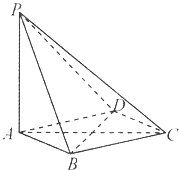 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.