题目内容
6.已知圆C:(x-a)2+(y-b)2=r2(a>0,r>0)与直线x=1相切,圆心C在直线4x-3y=0上,且到直线x-y-1=0的距离为$\sqrt{2}$.(1)求a,b,r的值;
(2)已知点A(-1,0),B(1,0),P是圆C上的任意一点,求|PA|2+|PB|2的最大值与最小值.
分析 (1)根据直线和圆的相切关系以及圆心到直线的距离关系建立方程关系即可求a,b,r的值;
(2)利用向量法结合数量积的应用即可得到结论.
解答 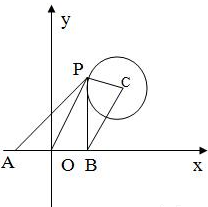 解:(1)若(x-a)2+(y-b)2=r2(a>0,r>0)与直线x=1相切,
解:(1)若(x-a)2+(y-b)2=r2(a>0,r>0)与直线x=1相切,
则|a-1|=r,
圆心C在直线4x-3y=0上,则4a-3b=0,即b=$\frac{4}{3}a$,
圆心到直线x-y-1=0的距离为$\sqrt{2}$.
则d=$\frac{|a-b-1|}{\sqrt{2}}$=$\sqrt{2}$,
即|a-b-1|=2,
则|a-$\frac{4}{3}a$-1|=2,
即|1+$\frac{a}{3}$|=2,
即1+$\frac{a}{3}$=2或1+$\frac{a}{3}$=-2,
解得a=3或a=-9(舍),
则b=4,r=|3-1|=2,
即a=3,b=4,r=2;
(2)设已知圆的圆心为C,由已知可得$\overrightarrow{OA}$=(-1,0),$\overrightarrow{OB}$=(1,0),
∴$\overrightarrow{OA}+\overrightarrow{OB}=0$,$\overrightarrow{OA}•\overrightarrow{OB}$=-1,
又由中点公式得$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PO}$,
∴|$\overrightarrow{PA}$|2+|$\overrightarrow{PB}$|2=($\overrightarrow{PA}+\overrightarrow{PB}$)2-2$\overrightarrow{PA}•\overrightarrow{PB}$=(2$\overrightarrow{PO}$)2-2($\overrightarrow{OA}-\overrightarrow{OP}$)•($\overrightarrow{OB}-\overrightarrow{OP}$)
=4|$\overrightarrow{PO}$|2-2$\overrightarrow{OA}$$•\overrightarrow{OB}$-2|$\overrightarrow{OP}$|2+2$\overrightarrow{OP}$•($\overrightarrow{OA}+\overrightarrow{OB}$)=2|$\overrightarrow{OP}$|2+2,
又∵$\overrightarrow{OC}$=(3,4),点P在圆(x-3)2+(y-4)2=4上,
∴|$\overrightarrow{OC}$|=5,|$\overrightarrow{CP}$|=2,且$\overrightarrow{OP}$=$\overrightarrow{OC}$+$\overrightarrow{CP}$,
∴|$\overrightarrow{OC}$|-|$\overrightarrow{CP}$|≤|$\overrightarrow{OP}$|=|$\overrightarrow{OC}+\overrightarrow{CP}$≤|$\overrightarrow{OP}$|+|$\overrightarrow{CP}$|,
即3≤|$\overrightarrow{OP}$|≤7,
故20≤|$\overrightarrow{PA}$|2+|$\overrightarrow{PB}$|2=2|$\overrightarrow{OP}$|2+2≤100,
∴|PA|2+|PB|2的最大值为100,最小值为20.
点评 本题主要考查圆的方程的应用以及两点间距离的应用,利用向量法是解决本题的关键.综合性较强,难度较大.

| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 直线 |
| A. | 恒为正值 | B. | 等于0 | C. | 恒为负值 | D. | 不大于0 |