题目内容
17.在等差数列{an}中,a3+a5=16,若对任意正整数n都有a1+a2+a3+…+an=an2+bn,其中a,b为常数,则128a+2b的最小值为32.分析 由题意和等差数列的性质可得7a+b=8,而128a+2b=27a+2b,由基本不等式可得.
解答 解:由题意可得a1+a2+a3+…+a7=49a+7b,
∴由求和公式和等差数列的性质可得$\frac{7({a}_{1}+{a}_{7})}{2}$
=$\frac{7}{2}$(a3+a5)=$\frac{7}{2}$×16=49a+7b,即7a+b=8,
∴128a+2b=27a+2b≥2$\sqrt{{2}^{7a+b}}$=32
当且仅当27a=2b即a=$\frac{4}{7}$且b=4时取等号,
故答案为:32
点评 本题考查等差数列的性质和求和公式,涉及基本不等式求最值,属基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.已知sin(π-α)=-2sin($\frac{π}{2}+α$),则$\frac{sinα+cosα}{sinα-cosα}$等于( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
12.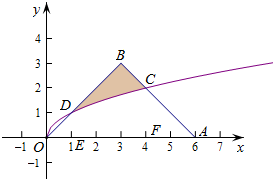 如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
 如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )
如图,等腰三角形OAB的顶点A、B的坐标分别为(6,0),(3,3),且AB与曲线y=$\sqrt{x}$交于点C,在△OAB中任取一点P,则点P落在阴影部分的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{27}$ | D. | $\frac{11}{54}$ |
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
9.二项式($\sqrt{x}$+$\frac{{4\sqrt{x}}}{x}$-4)4的展开式中常数项是( )
| A. | 3360 | B. | -1120 | C. | -3360 | D. | 1120 |
