题目内容
15．已知函数f（x）=|x-1|，且不等式f（x）+f（x+2）≤3的解集为M．若x∈M，|y|≤$\frac{1}{6}$，|z|≤$\frac{1}{9}$，求证：|x+2y-3z|≤$\frac{13}{6}$．分析 先求出M，再由条件利用绝对值不等式的性质可证得不等式．
解答 证明：不等式f（x）+f（x+2）≤3即|x-1|+|x+1|≤3，
x＜-1时，-x+1-x-1≤3，∴-1.5≤x＜-1；
-1≤x≤1时，-x+1+x+1≤3，∴-1≤x≤1；
x＞1时，x-1+x+1≤3，∴1＜x≤1.5，
∴|x|≤1.5
∵x∈M，|y|≤$\frac{1}{6}$，|z|≤$\frac{1}{9}$，
∴|x+2y-3z|≤|x|+2|y|+3|z|≤1.5+2×$\frac{1}{6}$+3×$\frac{1}{9}$=$\frac{13}{6}$，
∴：|x+2y-3z|≤$\frac{13}{6}$成立．
点评 本题主要考查绝对值的意义，绝对值不等式的解法，绝对值三角不等式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．设函数f（x）在R上存在导函数f′（x），对?x∈R，f（-x）+f（x）=x2，且当x∈（0，+∞），f′（x）＞x，若有f（1-a）-f（a）≥$\frac{1}{2}$-a，则实数a的取值范围为（ ）
| A． | （-∞，$\frac{1}{2}$] | B． | [$\frac{1}{2}$，+∞） | C． | （-∞，2] | D． | [2，+∞） |
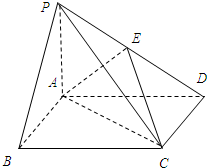在如图所示四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是正方式，PA=AB=1，E是PD上的点，PB∥平面AEC，