题目内容
11.已知实数x,y满足$\left\{\begin{array}{l}x+3y-3≤0\\ x-y+1≥0\\ y≥-1\end{array}\right.$,则点P(x,y)构成的区域的面积为8,2x+y的最大值为11,其对应的最优解为(6,-1).分析 先画出满足条件的平面区域,从而求出三角形的面积,令z=2x+y,变形为y=-2x+z,显然直线y=-2x+z过B(6,-1)时,z最大,进而求出最大值和最优解.
解答 解:画出满足条件的平面区域,如图示: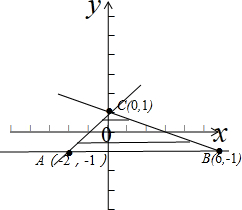 ,
,
∴点P(x,y)构成的区域的面积为:S△ABC=$\frac{1}{2}$×8×2=8,
令z=2x+y,则y=-2x+z,
当直线y=-2x+z过B(6,-1)时,z最大,
Z最大值=2×6-1=11,
∴其对应的最优解为(6,-1),
故答案为:8,11,(6,-1).
点评 本题考察了简单的线性规划问题,考察数形结合思想,是一道中档题.

练习册系列答案
相关题目
1.圆锥SO的侧面展开图为如图所示的半径为4的半圆,半圆中∠ASC=45°.
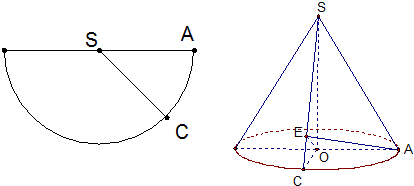
①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.

①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
19.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )
| A. | 4x-3y-19=0 | B. | 4x+3y-13=0 | C. | 3x-4y-16=0 | D. | 3x+4y-8=0 |