题目内容
16.已知函数f(x)=x${\;}^{-\frac{1}{2}}$-log3x,若x0是函数y=f(x)的零点,且0<x1<x0,则f(x1)( )| A. | 恒为正值 | B. | 等于0 | C. | 恒为负值 | D. | 不大于0 |
分析 根据函数的性质判断f(x)为减函数,再由x0是函数y=f(x)的零点,得到f(x0)=0,根据0<x1<x0,即可对f(x1)正负做出判断.
解答 解:根据指数函数与对数函数的性质可得:f(x)=x${\;}^{-\frac{1}{2}}$-log3x为减函数,
∵x0是函数y=f(x)的零点,
∴f(x0)=0,
∵0<x1<x0,
∴f(x1)>f(x0)=0.
故选:A.
点评 此题考查了函数零点的判定定理,以及函数的单调性,函数的零点的研究就可转化为相应方程根的问题,函数与方程的思想得到了很好的体现.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.设函数y=sin2x+$\sqrt{3}$cos2x的最小正周期为T,最大值为A,则( )
| A. | T=2π,A=2 | B. | T=2π,A=$\sqrt{2}$ | C. | T=π,A=2 | D. | T=π,A=$\sqrt{2}$ |

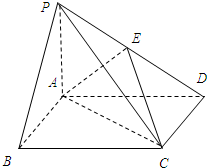 在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,
在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,