题目内容

14．在一张纸上画一个圆，圆心O，并在圆外设一点F，折叠纸圆上某点落于F点，设该点为M，抹平纸片，折痕AB，连接MO（或者OM）并延长交于AB于P，则P点轨迹为（　　）
A．椭圆B．双曲线C．抛物线D．直线

分析 根据ABC是线段MF的垂直平分线．可推断出|MP|=|PF|，进而可知|PO|-|PF|=|PO|-|PM|=|MO|结果为定值，进而根据双曲线的定义推断出点P的轨迹．

解答 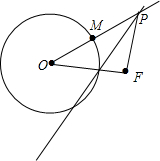解：由题意知，AB是线段MF的垂直平分线．
∴|MP|=|PF|，
∴|PO|-|PF|=|PO|-|PM|=|MO|（定值），
又显然|MO|＜|FO|，
∴根据双曲线的定义可推断出点P轨迹是以F、O两点为焦点的双曲线．
故选：B．

点评 本题主要考查了双曲线的定义的应用．考查了学生对双曲线基础知识的理解和应用．

练习册系列答案
相关题目
4．下列函数中，定义域为[1，+∞）的是（　　）
A．y=$\sqrt{x-1}$+$\sqrt{x+1}$B．y=（x-1）2C．y=（$\frac{1}{2}$）x-1D．y=ln（x-1）
5．已知F1（-c，0），F2（c，0）为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点，若椭圆上存在点P满足$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2c2，则此椭圆离心率的取值范围是[$\frac{1}{2}$，$\frac{\sqrt{3}}{3}$]．
2．已知A（1，2，1），B（-1，3，4），C（1，1，1），$\overrightarrow{AP}$=2$\overrightarrow{PB}$，则$\overrightarrow{PC}$=（　　）
A．（-$\frac{1}{3}$，$\frac{8}{3}$，3）B．（$\frac{1}{3}$，-$\frac{8}{3}$，-3）C．（-$\frac{4}{3}$，$\frac{5}{3}$，2）D．（$\frac{4}{3}$，-$\frac{5}{3}$，-2）
9．二项式（$\sqrt{x}$+$\frac{{4\sqrt{x}}}{x}$-4）4的展开式中常数项是（　　）
A．3360B．-1120C．-3360D．1120
19．过点P（4，-1）且与直线3x-4y+6=0垂直的直线方程是（　　）
A．4x-3y-19=0B．4x+3y-13=0C．3x-4y-16=0D．3x+4y-8=0
6．已知圆C：（x-a）2+（y-b）2=r2（a＞0，r＞0）与直线x=1相切，圆心C在直线4x-3y=0上，且到直线x-y-1=0的距离为$\sqrt{2}$．
（1）求a，b，r的值；
（2）已知点A（-1，0），B（1，0），P是圆C上的任意一点，求|PA|2+|PB|2的最大值与最小值．
3．己知f（x）=|x2-4x|+ax-2恰有2个零点，求a的范围．
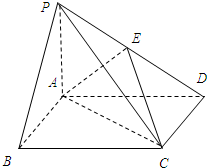4．在如图所示四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是正方式，PA=AB=1，E是PD上的点，PB∥平面AEC，
（Ⅰ）确定点E的位置并证明AE⊥PC
（Ⅱ）求三棱锥P-AEC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网