题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{-x}-2(x≤0)}\\{2ax-1(x>0)}\end{array}\right.$(a是常数,且a>0).对于下列命题:①函数f(x)的最小值是-1;②函数f(x)在R上是单调函数;③若f(x)>0在[$\frac{1}{2}$,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2,恒有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.其中正确命题的序号是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
分析 ①由图只需说明在点x=0处函数f(x)的最小值是-1;
②只需说明函数f(x)在R上的单调性即可;
③只需说明f(x)>0在[$\frac{1}{2}$,+∞)上恒成立,则当x=$\frac{1}{2}$时,函数取得最小值,从而求得a的取值范围是a>1;
④已知函数在(-∝,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,故D正确.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{e}^{-x}-2(x≤0)}\\{2ax-1(x>0)}\end{array}\right.$(a是常数,且a>0)的图象如下图所示: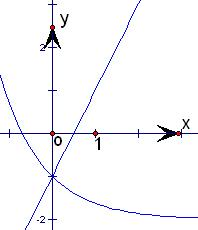
①由图可得:当x=0时,函数f(x)的最小值是-1;故正确;
②由图象说明函函数f(x)在R上不是单调函数;故错;
③若f(x)>0在[$\frac{1}{2}$,+∞)上恒成立,则f($\frac{1}{2}$)=a-1>0,求得a的取值范围是a>1;故正确;
④已知函数函数在(-∞,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,
即f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,故错误.
故正确命题的序号是:①③.
故选:B
点评 利用函数的图象研究函数的单调区间以及根据函数的增减性得到函数的最值是常用的方法,解答本题的关键是图象法.

练习册系列答案
相关题目
1.某中学为了研究学生的视力和座位(有关和无关)的关系,运用2×2列联表进行独立性研究,经计算K2=7.069,则至少有( )的把握认为“学生的视力与座位有关”.
附:
附:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
18.已知函数f(x)的定义域为实数R,f′(x)是其导函数,对任意实数x有f(x)+xf′(x)>0,则当a>b时,下列不等式成立的是( )
| A. | af(b)>bf(a) | B. | af(a)>bf(b) | C. | bf(a)>af(b) | D. | bf(b)>af(a) |
15.△ABC中,cos(A-B)+sin(A+B)=2,则△ABC的形状是( )
| A. | 等边三角形 | B. | 等腰钝角三角形 | C. | 等腰直角三角形 | D. | 锐角三角形 |