题目内容
7.曲线y=x3-4x与x轴所围成的封闭图形的面积是8.分析 首先画出围成的封闭图形,然后利用定积分表示出面积,最后计算定积分.
解答 解:曲线y=x3-4x与x轴所围成的封闭图形如图阴影部分,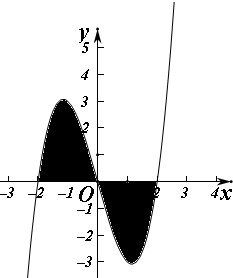 面积为2${∫}_{-2}^{0}({x}^{3}-4x)dx$=2($\frac{1}{4}{x}^{4}-2{x}^{2}$)|${\;}_{-2}^{0}$=8;
面积为2${∫}_{-2}^{0}({x}^{3}-4x)dx$=2($\frac{1}{4}{x}^{4}-2{x}^{2}$)|${\;}_{-2}^{0}$=8;
故答案为:8
点评 本题考查了利用定积分求曲边梯形的面积;一般的画出曲边梯形,利用定积分表示是关键,然后计算定积分.

练习册系列答案
相关题目
17.关于x的不等式x2-bx+c<0的解集为(-1,2),则方程x2-bx+2c=0的两根之积为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
18.有一个长为1km的斜坡,它的倾斜角为75°,现要将其倾斜角改为30°,则坡底要伸长( )
| A. | 1km | B. | $\sqrt{2}$km | C. | $\sqrt{3}$km | D. | 2km |
12.若N>1,logaN>logbN.且a+b=1,则有( )
| A. | 1<a<b | B. | 0<a<b<1 | C. | 1<b<a | D. | 0<b<a<1 |