题目内容
如果函数f(x)满足:对任意的实数x,y都有f(x+y)=f(x)•f(y)且f(1)=2,则
+
+
+
+…+
=______.
| f(2) |
| f(1) |
| f(4) |
| f(2) |
| f(6) |
| f(3) |
| f(8) |
| f(4) |
| f(20) |
| f(10) |
由f(x+y)=f(x)•f(y)得f(2x)=f(x)2⇒
=f(x).
∵f(x+y)=f(x)•f(y)⇒f(x+1)=f(x)•f(2)=2f(x)⇒
=2,
所以数列{f(n)}是以2为首项,2为公比的等比数列,故f(n)=2×2n-1=2n.
∴
=f(n)=2n.
则
+
+
+
+…+
=21+22+23+…+210=
=211-2=2046.
故答案为:2046.
| f(2x) |
| f(x) |
∵f(x+y)=f(x)•f(y)⇒f(x+1)=f(x)•f(2)=2f(x)⇒
| f(x+1) |
| f(x) |
所以数列{f(n)}是以2为首项,2为公比的等比数列,故f(n)=2×2n-1=2n.
∴
| f(2n) |
| f(n) |
则
| f(2) |
| f(1) |
| f(4) |
| f(2) |
| f(6) |
| f(3) |
| f(8) |
| f(4) |
| f(20) |
| f(10) |
| 2(1-210) |
| 1-2 |
故答案为:2046.

练习册系列答案
相关题目
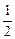 )
)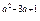 的单调递减区间.
的单调递减区间.
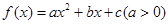 与
与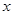 轴的两个交点的横坐标分别为1和3,则不等式
轴的两个交点的横坐标分别为1和3,则不等式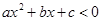 的解集是 .
的解集是 .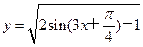 的单调递减区间为 .
的单调递减区间为 .