题目内容
2.若函数f(x)=tan($\frac{π}{4}$+x),则f($\frac{π}{3}$)=( )| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | -2-$\sqrt{3}$ |
分析 根据已知中函数的解析式,将x=$\frac{π}{3}$代入,结合两角和的正切公式,可得答案.
解答 解:∵f(x)=tan($\frac{π}{4}$+x),
∴f($\frac{π}{3}$)=tan($\frac{π}{4}$+$\frac{π}{3}$)=$\frac{tan\frac{π}{4}+tan\frac{π}{3}}{1-tan\frac{π}{4}tan\frac{π}{3}}$=$\frac{1+\sqrt{3}}{1-\sqrt{3}}$=-2-$\sqrt{3}$.
故选:D.
点评 本题考查的知识点是正切函数的图象,两角和的正切公式,直接代入求值即可,属于基础题.

练习册系列答案
相关题目
10.如果点P(sinθ+cosθ,sinθcosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.光线从A(-3,4)点射出,到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,6),则BC所在直线的方程为( )
| A. | 5x-2y+7=0 | B. | 2x-5y+7=0 | C. | 5x+2y-7=0 | D. | 2x+5y-7=0 |
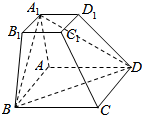 如图在四棱台ABCD-A1B1C1D1中,AA1⊥平面ABCD,两底面均为正方形,AB=AA1=2A1B1.
如图在四棱台ABCD-A1B1C1D1中,AA1⊥平面ABCD,两底面均为正方形,AB=AA1=2A1B1.