题目内容
12.在△ABC中,A,B,C所对的边分别为a,b,c,2c2-2a2=b2(1)求$\frac{ccosA-acosC}{b}$的值;
(2)若a=1,tanA=$\frac{1}{3}$,求△ABC的面积S.
分析 (1)利用余弦定理结合2c2-2a2=b2得到ccosA-acosC=$\frac{b}{2}$,代入$\frac{ccosA-acosC}{b}$得答案;
(2)利用正弦定理把(1)结论中边转化成角的正弦,进而利用两角和公式化简整理,可求得sinCcosA
=3sinAcosC,进而求得tanC和tanA的关系,求得tanC,得到C.再由正弦定理求出边c,则三角形面积可求.
解答 解:(1)∵2c2-2a2=b2,
∴ccosA-acosC=$c•\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}-a•\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$
=$\frac{2{c}^{2}-2{a}^{2}}{2b}=\frac{{b}^{2}}{2b}=\frac{b}{2}$,
∴$\frac{ccosA-acosC}{b}$=$\frac{\frac{b}{2}}{b}=\frac{1}{2}$;
(2)由(1)和正弦定理以及sinB=sin(A+C),
得2sinCcosA-2sinAcosC=sinAcosC+cosAsinC,
即sinCcosA=3sinAcosC,
又cosAcosC≠0,∴tanC=3tanA=1,故C=45°.
由tanA=$\frac{1}{3}$,得cotA=3,
∴sinA=$\frac{1}{cscA}=\frac{1}{\sqrt{1+co{t}^{2}A}}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{10}$,cosA=$\frac{3\sqrt{10}}{10}$.
又a=1,∴$\frac{1}{\frac{\sqrt{10}}{10}}=\frac{c}{sin45°}=\frac{c}{\frac{\sqrt{2}}{2}}$,解得$c=\sqrt{5}$.
又sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{\sqrt{10}}{10}×\frac{\sqrt{2}}{2}+\frac{3\sqrt{10}}{10}×\frac{\sqrt{2}}{2}=\frac{2\sqrt{5}}{5}$.
∴△ABC的面积S=$\frac{1}{2}×1×\sqrt{5}×\frac{2\sqrt{5}}{5}=1$.
点评 本题主要考查了正弦定理和余弦定理的运用.解题的关键是对正弦定理和余弦定理能熟练灵活的运用,是中档题.

 金博士一点全通系列答案
金博士一点全通系列答案| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | -2-$\sqrt{3}$ |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
 已知函数f(x)=2sin(2x+$\frac{π}{6}$)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=2sin(2x+$\frac{π}{6}$)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )| A. | ω=2 | |
| B. | f($\frac{π}{3}$)=1 | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象 |
 ,定直线
,定直线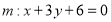 ,过
,过 的一条动直线
的一条动直线 与直线相交于
与直线相交于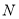 ,与圆
,与圆 相交于
相交于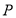 ,
,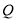 两点,
两点,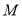 是
是 中点.
中点.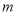 垂直时,求证:
垂直时,求证: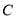 ;
;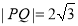 时,求直线
时,求直线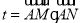 ,试问
,试问 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出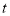 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.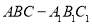 中,底面为直角三角形,
中,底面为直角三角形, ,
,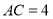 ,
,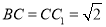 ,
,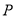 是
是 上一动点,则
上一动点,则 的最小值是_____.
的最小值是_____.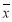 和样本方差
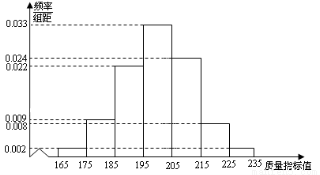
和样本方差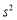 (用同一组数据用该区间的中点值用代表);
(用同一组数据用该区间的中点值用代表);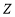 服从正态分布
服从正态分布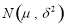 ,其中
,其中 近似为样本平均数
近似为样本平均数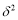 近似为样本方差
近似为样本方差 .
. ;
;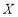 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数,利用(i)的结果,求
的产品件数,利用(i)的结果,求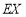 .
.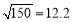 ,若
,若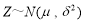 ,则
,则 ,
,
 ,则
,则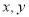 不全为零”的否命题;
不全为零”的否命题;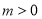 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;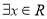 ,
,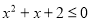 ”的否定.
”的否定.