题目内容
12.(1)计算:log3$\frac{\root{4}{27}}{3}$+lg25+lg4+${log_7}{7^2}$+log23•log34;(2)设集合A={x|$\frac{1}{32}$≤2-x≤4},B={x|m-1<x<2m+1}.若A∪B=A,求m的取值范围.
分析 (1)根据对数的运算性质即可求出,
(2)先化简集合A,在分类讨论即可求出m的范围.
解答 解:(1)log3$\frac{\root{4}{27}}{3}$+lg25+lg4+${log_7}{7^2}$+log23•log34=$lo{g}_{3}{3}^{-\frac{1}{4}}$+lg100+2+$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$=-$\frac{1}{4}$+2+2+2=$\frac{23}{4}$.
(2)设集合A={x|$\frac{1}{32}$≤2-x≤4}=[-2,5],B={x|m-1<x<2m+1}.
∵A∪B=A,
∴B⊆A,
当B=∅时,即m-1≥2m+1时,解得m≤-2,满足题意,
当B≠∅时,则$\left\{\begin{array}{l}{m-1<2m+1}\\{m-1≥-2}\\{2m+1≤5}\end{array}\right.$解得-1≤m≤2,
综上所述m的取值范围为(-∞,-2]∪[-1,2]
点评 本题考查了对数的运算和性质和集合与集合之间的关系,属于基础题.

练习册系列答案
相关题目
20.数列{an}满足an=4an-1+3且a1=0,则此数列第4项是( )
| A. | 15 | B. | 16 | C. | 63 | D. | 255 |
7.直线$3x+\sqrt{3}y-a=0$的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
17.某三棱锥的三视图如图所示,该三棱锥的最长棱的棱长为( )
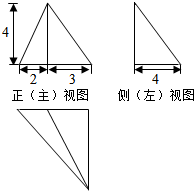

| A. | $\sqrt{61}$ | B. | $\sqrt{41}$ | C. | 2$\sqrt{5}$ | D. | 5 |
1.已知集合A={(x,y)|$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{x+y≥2}\end{array}\right.$},B={(x,y)|(x+1)2+(y+1)2≤$\frac{4}{5}$},设P(m,n)∈A,Q(s,t)∈B,则$\frac{n-t}{m-s}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
2.若函数f(x)=tan($\frac{π}{4}$+x),则f($\frac{π}{3}$)=( )
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | -2-$\sqrt{3}$ |