题目内容
【题目】已知椭圆![]() 的对称中心为原点
的对称中心为原点![]() ,焦点在
,焦点在![]() 轴上,焦距为
轴上,焦距为![]() ,点
,点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆![]() 的方程;
的方程;
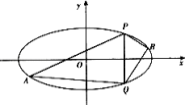
(2)直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 点位于第一象限,
点位于第一象限,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当点
两侧的动点.当点![]() 运动时,满足
运动时,满足![]() ,问直线
,问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题可得![]() ,
,![]() 所以
所以![]() ,则椭圆
,则椭圆![]() 的方程为
的方程为![]()
(2)将![]() 代入椭圆方程可得
代入椭圆方程可得![]() ,解得
,解得![]() ,则
,则![]() ,由题可知直线
,由题可知直线![]() 与直线
与直线![]() 的斜率互为相反数,写出直线
的斜率互为相反数,写出直线![]() 的方程与椭圆方程联立整理可得
的方程与椭圆方程联立整理可得![]() 。
。
(1)因为椭圆![]() 的对称中心为原点
的对称中心为原点![]() ,焦点在
,焦点在![]() 轴上,
轴上,
所以设椭圆方程为![]()
因为焦距为![]() ,
,
所以![]() ,焦点坐标
,焦点坐标![]() ,
,![]()
又因为点![]() 在该椭圆上,代入椭圆方程得
在该椭圆上,代入椭圆方程得
所以![]() ,即
,即![]()
解得![]()
所以![]()
则椭圆![]() 的方程为
的方程为![]() .
.
(2)将![]() 代入椭圆方程可得
代入椭圆方程可得![]() ,解得
,解得![]()
则![]()
当点![]() 运动时,满足
运动时,满足![]() ,则直线
,则直线![]() 与直线
与直线![]() 的斜率互为相反数,
的斜率互为相反数,
不妨设![]() ,则
,则![]() ,
,![]()
所以直线![]() 的方程为
的方程为![]() ,
,
联立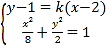 ,解得
,解得![]()
因为![]() 是该方程的两根,
是该方程的两根,
所以![]() ,即
,即![]() ,
,
同理直线![]() 的方程为
的方程为![]() 且
且![]()
所以![]()
所以![]() ,
,
即直线![]() 的斜率为定值。
的斜率为定值。

练习册系列答案
相关题目
【题目】为了研究高二阶段男生、女生对数学学科学习的差异性,在高二年级所有学生中随机抽取25名男生和25名女生,计算他们高二上学期期中、期末和下学期期中、期末的四次数学考试成绩的各自的平均分,并绘制成如图所示的茎叶图.
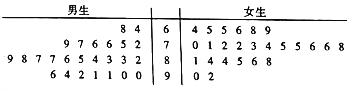
(1)请根据茎叶图判断,男生组与女生组哪组学生的数学成绩较好?请用数据证明你的判断;
(2)以样本中50名同学数学成绩的平均分x0(79.68分)为分界点,将各类人数填入如下的列联表:
分数 性别 | 高于或等于x0 | 低于x0 | 合计 |
男生 | |||
女生 | |||
合计 |
(3)请根据(2)中的列联表,判断能否有99%的把握认为数学学科学习能力与性别有关?
附:K2=![]()
P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |