Question

【题目】集合A= ，若BA求m的取值范围．

Answer 1

【答案】解：集合A中的不等式组得：集合A={x|﹣2＜x＜5}，
进而分2种情况讨论：
①B=Ф，此时符合BA，
若m+1＞2m﹣1，解可得m＜2，
此时，m＜2；
②B≠Ф，即m+1≤2m﹣1时，
要使BA，
则 ，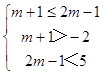
解得：2≤m＜3，
综合①②得m的取值范围是{m|m＜3}
【解析】根据题意，解集合A中的不等式组，可得集合A={x|﹣2＜x＜5}，进而对m分2种情况讨论：①B=Ф，即m+1＞2m﹣1时，解可得m的范围，②B≠Ф，即m+1≤2m﹣1时，要使BA，必有则 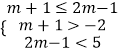，解可得m的取值范围，综合2种情况即可得答案．
【考点精析】解答此题的关键在于理解子集与真子集的相关知识，掌握任何一个集合是它本身的子集；n个元素的子集有2n个,n个元素的真子集有2n －1个,n个元素的非空真子集有2n－2个．