题目内容
【题目】已知两个不共线的向量![]() ,
,![]() 夹角为
夹角为![]() ,且
,且![]() ,
,![]() ,为正实数.
,为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及对应的x的值,并指出此时向量
的最小值及对应的x的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数m,关于x的方程
为锐角,对于正实数m,关于x的方程![]() 两个不同的正实数解,且
两个不同的正实数解,且![]() ,求m的取值范围.
,求m的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,垂直;(3)
,垂直;(3)![]() 时,
时,![]() ,
,![]() 时,
时,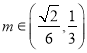 ,
,
![]() 时,
时,![]() .
.
【解析】
(1)根据垂直关系计算得到![]() ,再根据向量夹角公式得到答案.
,再根据向量夹角公式得到答案.
(2)计算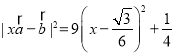 ,根据二次函数性质得到最值,计算
,根据二次函数性质得到最值,计算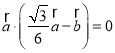 得到位置关系.
得到位置关系.
(3)根据题意平方得到二次方程,根据根与系数关系得到范围,讨论![]() 和
和![]() ,
,![]() 三种情况,计算得到答案.
三种情况,计算得到答案.
(1)![]() ,故
,故![]() ,
,
故![]() ,故
,故![]() .
.
(2)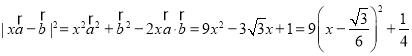 ,
,
当![]() 时,
时,![]() 最小为
最小为![]() ,故
,故![]() 的最小值为
的最小值为![]() ,
,
此时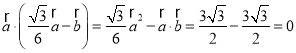 ,故向量
,故向量![]() 与
与![]() 垂直.
垂直.
(3)![]() ,即
,即![]() ,展开整理得到
,展开整理得到![]() ,
,
故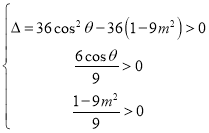 ,且
,且![]() ,解得
,解得![]() .
.
取![]() 得到
得到![]() ,即
,即![]() ,
,
当![]() ,即
,即![]() ,即
,即![]() 时,
时,![]() ;
;
当![]() ,即
,即![]() 且
且![]() ,即
,即![]() 时,
时,
![]() ;
;
当![]() ,即
,即![]() ,即
,即![]() 时,
时,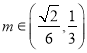 .
.
综上所述:![]() 时,
时,![]() ,
,![]() 时,
时,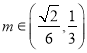 ,
,
![]() 时,
时,![]() .
.

练习册系列答案
相关题目